|
|
Applications
of differentiation - the graph of a function and its derivatives |
Maclaurin's
formula or Maclaurin's theorem |
|
The
approximation of the sine function
by polynomial using Taylor's or Maclaurin's formula |
|
Properties
of the power series expansion of the sine function |
|
|
|
|
|
|
|
| Maclaurin's
formula or Maclaurin's
theorem |
| The
formula obtained from
Taylor's
formula by setting x0
= 0
|
 |
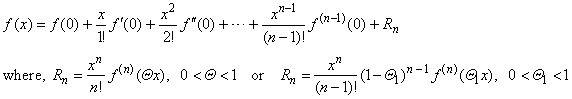| that
holds in an open neighborhood of the origin, is called Maclaurin's
formula or Maclaurin's
theorem. |
|
| Consider
the polynomial
fn
(x)
= anxn
+ an -
1xn -
-
1 + · · · + a3x3
+ a2x2 + a1x
+ a0, |
| let
evaluate the polynomial and its successive derivatives at the origin, |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . .
, f (n) (0) =
n! an |
| we
get the coefficients, |
 |
|
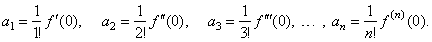| Therefore,
the Taylor polynomial of a function f
centered at x0
is the polynomial of degree n
which has the same
derivatives as f
at x0,
up to order n. |
| If
a
function f
is infinitely differentiable on an interval about a point x0
or the origin, as are for example ex and
sin
x,
then |
|
P0 (x)
= f (x0), |
|
P1 (x) =
f (x0)
+ (x
-
x0)
f ' (x0), |
|
|
| P0,
P1,
P2,
. . . is a sequence of increasingly approximating polynomials for
f. |
|
|
| The
approximation of the sine function
by polynomial using Taylor's or Maclaurin's formula |
| Example: Let
represent the sine function f
(x)
= sin x
by the Taylor polynomial (or power series). |
| Solution: The
sine function is the infinitely differentiable function defined
for all real numbers. |
| We
use the polynomial with infinitely many terms
|
 |
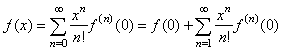| to
represent the sine function. We should calculate the function
value f(0),
and some successive derivatives of
the sine function, to determine the nth
order derivative expression, therefore
|
 |
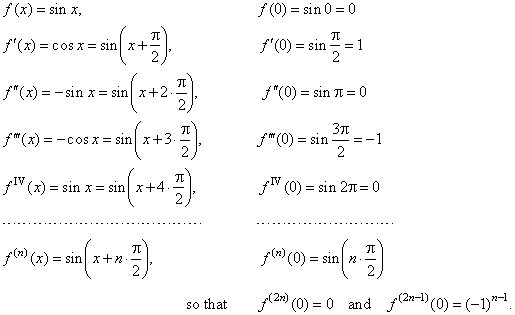| Obtained
values f(0)
and f (n)(0)
substituted into Maclaurin's formula with Lagrange
remainder
yield, |
 |
 |
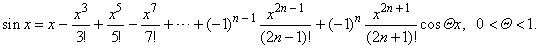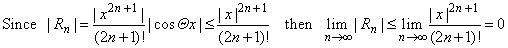| thus, |
 |
|
|
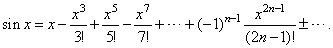Properties
of the power series expansion of the sine function |
| The polynomials that describe the sine function
all are symmetric source polynomials of odd degree. Meaning, |
| both coordinates
of translations |
 |
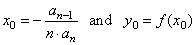are
zero since all even derivatives are |
|
| zero, the infinite polynomial is missing
every next even term, therefore an-1
= 0. |
 |
 |
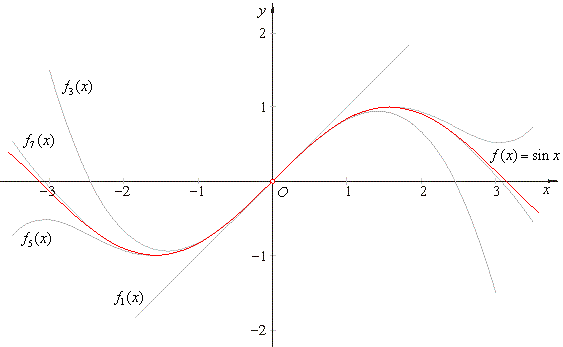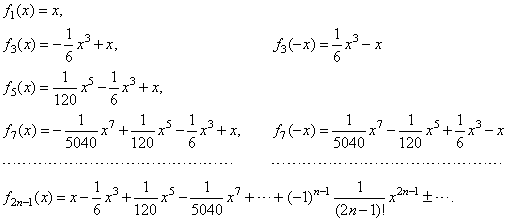| Notice
that every second polynomial in the above sequence, whose leading term
is negative, represents the variant f
(-x)
(or -
f (x))
of the source polynomial of odd degree whose x
or y
variable changed the sign, as are
the graphs, f3
(x)
and f7 (x). |
| Observe that graphs
of polynomials
approach closer and closer to the graph of sine function as n
increase. |
|
|
|
|
|
