|
|
|
|
Applications
of differentiation - the graph of a function and its derivatives |
Taylor's
theorem (Taylor's
formula) - The extended mean value theorem |
|
The proof of Thaylor's theorem |
|
Maclaurin's
formula or Maclaurin's theorem |
|
Representing
polynomial using Maclaurin's and Taylor's formula |
|
Representing
polynomial using Maclaurin's and Taylor's formula examples |
|
|
|
|
|
|
| Taylor's
theorem (Taylor's
formula) - The extended mean value theorem |
| Suppose
f
is continuous
on the closed interval [x0,
x0
+ h]
with continuous
derivatives to
(n
-
1)th
order on the
interval and its nth
derivative defined on
(x0,
x0
+ h)
then, |
 |
|
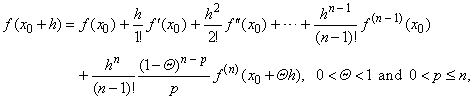is called Taylor's theorem. |
|
To prove Taylor's theorem we
substitute x0
= a,
x0
+ h = b
and introduce the function |
 |
|
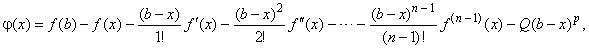where Q
is still undetermined and p
> 0. |
| Since
j
(b) = 0
we
can define
Q
by setting j
(a)
= 0
too, |
 |
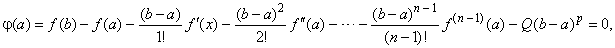| then
we compute j
' (x)
to apply Rolle's
theorem. |
| Note
that successive terms cancel (by the product rule) when differentiating j
(x), so we get |
 |
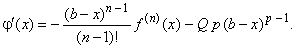| Thus,
by Rolle's theorem there is some intermediate point c
inside the interval [a,
b]
such that j'
(c)
= 0, |
 |
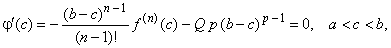| which
gives |
 |
|
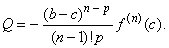| By
plugging the Q
back into above equation j
(a)
= 0
while returning substitutions, |
| a
= x0,
b
= x0
+ h,
b
-
a
= h
and where |
 |
|
|
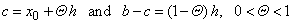| we
obtain Taylor's theorem to be proved. |
| The
last term in Taylor's formula |
|
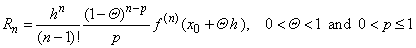
| is
called the remainder and denoted Rn
since it follows after n
terms. |
| By
plugging, a) p
= n into
Rn
we get |
 |
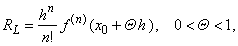| the
Lagrange
form of the remainder, |
|
while if b) p
= 1
we get |
 |
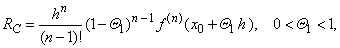| the
Cauchy
form of the remainder. |
| Thus,
by substituting x0
+ h = x
obtained is |
 |
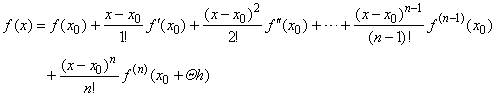| Taylor's
formula with Lagrange form of the remainder. |
| Therefore, Taylor's
formula gives values of a function f
inside the interval [x0,
x0
+ h]
using its value and the values
of its derivatives to
(n
-
1)th
order at the point x0 in the form |
| f (x) =
Pn -
1(x
-
x0) + R n |
| where,
Pn
-
1(x
-
x0)
is
(n
-
1)th
order Taylor polynomial for f
given by the first n
terms in the above
formula and Rn
is one of the given remainders. |
|
| Maclaurin's
formula or Maclaurin's
theorem |
| The
formula obtained from
Taylor's
formula by setting x0
= 0
|
 |
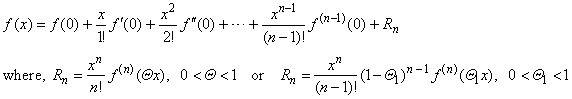| that
holds in an open neighborhood of the origin, is called Maclaurin's
formula or Maclaurin's
theorem. |
|
| Consider
the polynomial
fn
(x)
= anxn
+ an -
1xn -
-
1 + · · · + a3x3
+ a2x2 + a1x
+ a0, |
| let
evaluate the polynomial and its successive derivatives at the origin, |
| f
(0) =
a0, f '(0) = 1· a1,
f ''(0) = 1· 2a2,
f '''(0) = 1· 2· 3a3, . . .
, f (n)(0) =
n!an |
| we
get the coefficients, |
 |
|
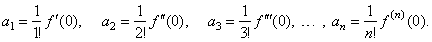| Therefore,
the Taylor polynomial of a function f
centered at x0
is the polynomial of degree n
which has the same
derivatives as f
at x0,
up to order n. |
| If
a
function f
is infinitely differentiable on an interval about a point x0
or the origin, as are for example ex and
sin
x,
then |
|
P0 (x)
= f (x0), |
|
P1 (x) =
f (x0)
+ (x
-
x0)
f ' (x0), |
|
|
| P0,
P1,
P2,
. . . is a sequence of increasingly approximating polynomials for
f. |
|
| Representing
polynomial using Maclaurin's and Taylor's formula |
| If
given is an n-th
degree polynomial |
| Pn(x) =
anxn + an -
1xn -
1 + ·
· · + a2x2
+ a1x + a0 then, |
| Pn(0) =
a0,
Pn' (0) = a1,
Pn''(0) = 2!
a2,
Pn'''(0) = 3!
a3,
. . . , Pn(n)(0) = n!
an
and
Pn(n
+ 1) = 0 |
| so,
the coefficients of the polynomial |
 |
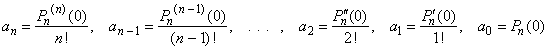| therefore,
applying Maclaurin's formula, every polynomial can be written as |
 |
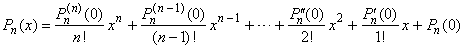| since
Pn(n
+ 1) = 0,
the remainder vanishes. |
|
| Representing
polynomial using Maclaurin's and Taylor's formula, examples |
| Example: Represent
the quintic y
= 2x5 + 3x4 -
5x3 + 8x2 -
9x + 1 using Maclaurin's
formula. |
| Solution: Let write
all successive derivatives of the given quintic and evaluate them at the
origin, |
|
y' (x)
= 10x4 + 12x3 -
15x2 + 16x -
9,
y' (0)
= -
9 |
|
y'' (x)
= 40x3 + 36x2 -
30x + 16,
y'' (0)
= 16 |
|
y''' (x)
= 120x2 + 72x -
30,
y''' (0)
= -
30 |
|
yIV
(x)
= 240x + 72,
yIV
(0)
= 72 |
|
yV
(x)
= 240,
yV
(0)
= 240 |
|
yVI
= 0 and the last term of the polynomial a0
= y(0)
= P5(0) =
1, |
| then
substitute obtained values into Maclaurin's
formula |
 |
|
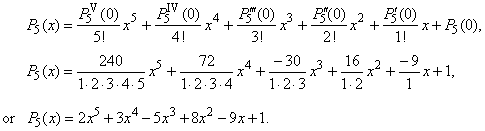| Example: Represent
the quartic y
= x4 -
4x3 + 4x2 + x -
4 at x0
= 2 using
Taylor's
formula. |
| Solution: Let write
all successive derivatives of the given quartic and evaluate them at x0
= 2, |
|
y' (x)
= 4x3 -
12x2 + 8x + 1,
y' (2)
= 1 |
|
y'' (x)
= 12x2 -
24x + 8,
y'' (2)
= 8 |
|
y''' (x)
= 24x -
24,
y''' (2)
= 24 |
|
yIV
(x)
= 24,
yIV
= 24 |
|
yV
(x)
= 0
and the last term, a0
=
y(2)
= P4(2) = -
2, |
| then
substitute obtained values into Taylor's
formula |
 |
|
|
|
|
|
|
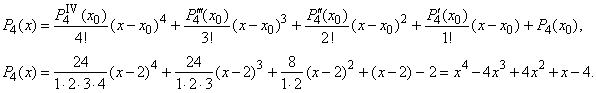