|
|
|
|
Differential calculus - derivatives |
 The chain rule
The chain rule |
|
Differentiation using the chain rule, examples |
|
|
|
|
|
|
| The
chain rule |
| If
y = f (u)
and u
= g (x)
such that f
is differentiable at u
= g (x) and g
is differentiable at x,
that is, |
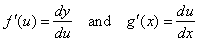
|
| then,
the composition of f
with g, |
| y
= (
f o g
)(x)
= f [g (x)] |
|
is differentiable at x,
and then |
|
|
|
Thus,
the derivative of a composition of functions is equal to the
derivative of outside function, with respect to
|
| the
inside function (i.e., taking it as the independent variable),
times the derivative of the inside function. |
|
| Differentiation
using the chain rule, examples |
| Example: |
Find
the derivative of the function |
y =
(x2 -
3x + 5)3. |
|
| Solution: |
Consider
y = f
[g
(x)]
where, y = f
(u) =
u3
and u
= g (x) =
x2 -
3x + 5 |
|
|
so
that,
|
|
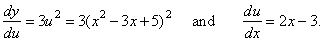 |
|
|
|
Therefore,
|
|
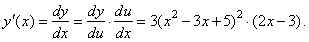 |
|
|
|
| Example: |
Find
the derivative of the function |
y =
sin3 2x = (sin 2x)3. |
|
| Solution: |
Consider
y = f
{g [h(x)]}
where, y = f
(u) =
u3,
u
= g(v) = sin v
and v
= h(x) = 2x. |
|
|
so
that,
|
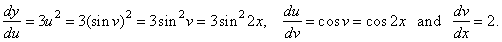 |
|
|
Therefore,
|
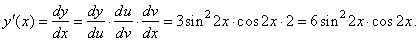 |
|
|
|
| Example: |
Find
the derivative of the function |
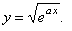 |
|
| Solution: |
Consider
y = f
{g [h (x)]}
where, |
|
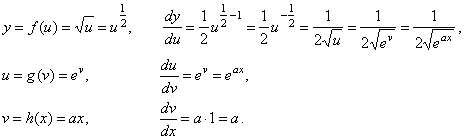
|
|
Therefore,
|
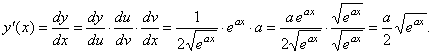 |
|
|
| Example: |
Find
the derivative of the function |
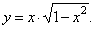 |
|
| Solution: |
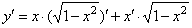 |
|
|
|
| Remember,
if |
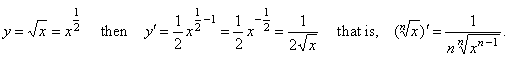 |
|
|
|
| Example: |
Find
the derivative of the function |
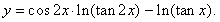 |
|
| Solution: |
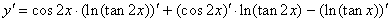 |
|
|
|
|
|
| Example: |
Find
the derivative of the function |
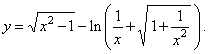 |
|
| Solution: |
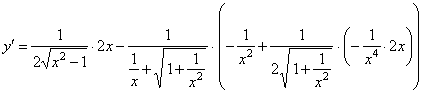 |
|
|
|
| Remember,
if |
|
|
|
| therefore,
if |
|
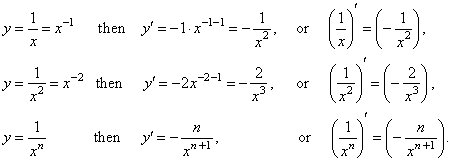 |
|
|