Differential calculus - derivatives

Derivatives of basic or elementary functions

The derivative of the sine function

The derivative of the cosine function

The derivative of the exponential function

The derivative of the logarithmic function

We use the limit definition

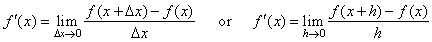to find the derivative of a function.

The derivative of the sine function

We use the limit of the difference quotient to find the derivative of the function  f (x) = sin x.

Let rewrite the difference quotient applying the sum to product formula,

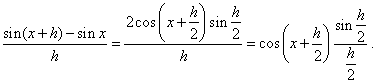Since, the derivative is the limit of the difference quotient as h tends to zero then,

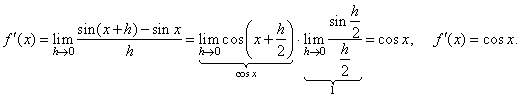Therefore, if f(x) = sin x  then

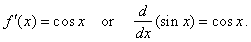The derivative of the cosine function

We use the limit of the difference quotient to find the derivative of the function  f (x) = cos x.

Let rewrite the difference quotient applying the sum to product formula,

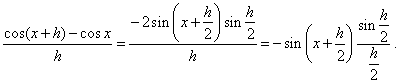Since the derivative is the limit of the difference quotient as h tends to zero then,

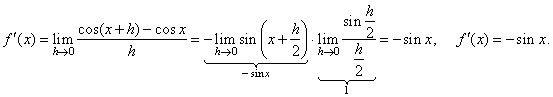Therefore, if f (x) = cos x  then

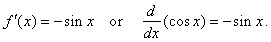The derivative of the exponential function

Let use the limit of the difference quotient to find the derivative of the function  f (x) = ax.

Since the difference quotient is

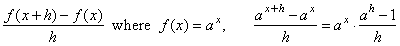then, the derivative as the limit of the difference quotient as h tends to zero

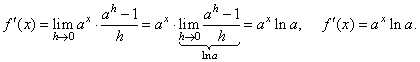That is, by plugging  t = ah - 1, then  t ® 0 as  h ® 0, and

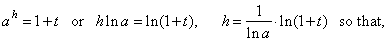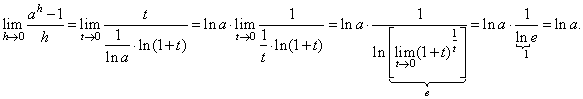Therefore, if f (x) = ax  then

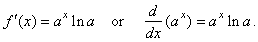or when the base a is substituted by the natural base e obtained is the exponential function  ex, thus

if f (x) = ex  then

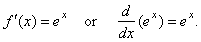The derivative of the logarithmic function

Let's use the limit of the difference quotient to find the derivative of the function  f (x) = loga x.

The difference quotient applied to the given function

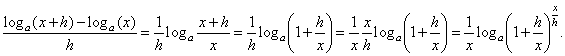As the derivative is the limit of the difference quotient as h tends to zero, then

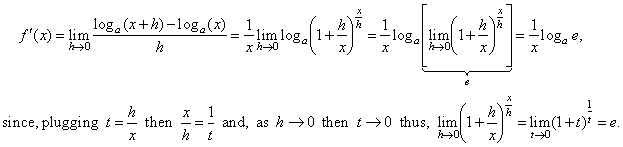Then, applying the base change identity and substituting  a = e

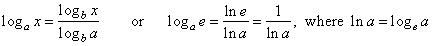if    f (x) = loga x then

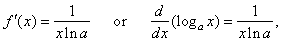if    f (x) = ln x then

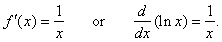Calculus contents C

Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.