|
| Differential
calculus |
|
|
|
|
Differential
Calculus
- Derivatives and differentials |
The derivative of a
function |
|
Definition of the derivative of a function |
|
Tangent to
a curve |
|
The
equation of the line tangent to the given curve at the given point |
|
Determining the derivative of a function as the limit of the
difference quotient |
|
The
equation of the line tangent to the given curve at the given point
example |
|
|
|
|
|
|
|
|
| The
derivative of a function |
|
The
slope or the gradient of the secant line joining points (x,
f (x)) and (x
+ Dx,
f (x + Dx))
given by |
|
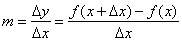
| is
called the difference quotient, and
represents the average rate of change of the function y
= f (x). |
|
|
Note
that in the above equation x
is the given fixed point and the only variable quantity is the
distance increment,
Dx.
|
|
|
|
Definition of the derivative of a function |
|
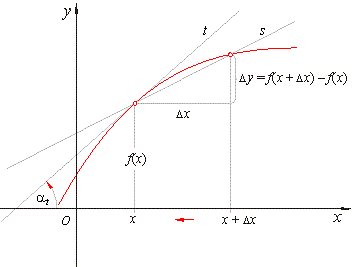
As
the distance
Dx
gets smaller, the average rate of change
becomes more accurate, that is the secant line becomes
more and more like the tangent line of the curve at the point
(x,
f (x)),
as shows the figure above.
|
| Therefore,
the limit of the difference quotient as Dx
®
0,
that
equals
the slope of the line tangent to the curve at
the
point (x,
f (x)),
|
 |
|
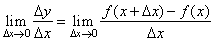represents the instantaneous rate of change of the function
with respect to x,
or when written as
|
|
|
|
where
Dx
is substituted with h,
is
called the derivative of a function
f
at a given point x.
|
|
Geometrically,
the derivative is the slope m
(gradient) of the tangent at the point (x,
y) to the curve y
= f (x).
|
| There
are other common notations for the derivative like, |
 |
|
|
|
|
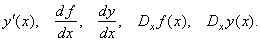| The
equation of the line tangent to the given curve at the given point |
| The
equation of the tangent line at the given point (x0,
y0) of a function y
= f (x) we write using the
point slope
equation of a line, |
|
y
-
y0
= f
'
(x0) · (x
-
x0)
|
| where
m = f '
(x0)
is the slope of the tangent line at
the point
(x0,
y0).
|
|
|
|
Determining the derivative of a function as the limit of the
difference quotient |
| Example: Find
the equation of the tangent line at the point (2,
4)
of the function f
(x)
= x2.
|
|
| Solution: The
slope of the tangent line at
the given point
we calculate using
the formula |
|
|
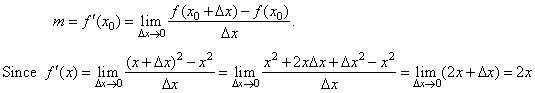
| then, |
| m
= f '
(x0)
= 2x0,
m
= f '
(2)
= 2 · 2
= 4. |
| By
substituting m
= 4 and the point (2,
4) into |
| y
-
y0
= f
'
(x0) · (x -
x0), |
| we
get |
| y
-
4
= 4 · (x -
2) or
y
= 4x -
4 |
| the
equation of the tangent line at the given point
of the function f
(x)
= x2, as shows the
right figure.
|
|
 |
|
|
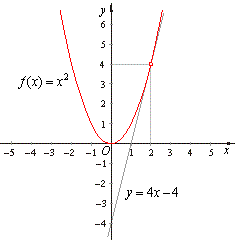