|
| Coordinate
Geometry (Analytic Geometry) in Three-dimensional Space |
|
|
Line
and Plane
|
|
Points, Lines and planes relations in 3D space, examples
|
 The angle between line and plane
The angle between line and plane
|
|
|
|
|
|
|
| Points, Lines and planes relations
in 3D space, examples
|
| Example:
Through a line which is written as the intersection of two planes, P1
::
x -
2y
+ 3z -
4 = 0 and
P2
::
3x + y
-
z + 1 = 0, lay a plane which passes through the point
A(-
1,
2,
1).
|
| Determine the equation of the plane. |
| Solution: Write the equation of a sheaf,
P1
+ lP2 = 0
or (x - 2y
+
3z -
4)
+ l(3x +
y -
z + 1) = 0. |
| Plug
the point A
into the equation to determine l
such that the plane passes through the given point, so |
| A(-1,
2,
1)
=>
P1
+ lP2 = 0
gives (-1
- 2 · 2 +
3 · 1 -
4)
+ l[3 · (-1) +
2 -
1 + 1] = 0, l =
-
6. |
| Therefore,
(x - 2y
+
3z -
4) -
6 · (3x + y -
z + 1) = 0
or -
17x -
8y
+ 9z -
10 = 0 |
| is the plane passing through
the given line and the point A. |
|
| Example:
Through the line |
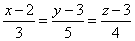 |
lay
a plane to be parallel to the
y-axis, determine
|
|
| the
equation of the plane. |
| Solution: Write the line as the intersection of two planes to be able to form the sheaf of planes, therefore
|
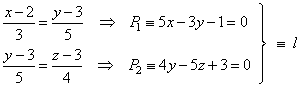 |
| P1 and
P2
are the planes of which the given line is intersection and which are perpendicular to the coordinate
planes,
xy
and yz
respectively.
|
| Form the equation of a sheaf to determine the parameter
l according to
the given condition |
| P1
+ lP2 = 0
or (5x
-
3y -
1)
+ l(4y
-
5z + 3) = 0 |
| then,
5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
and Ns
= 5i + (-
3
+ 4l)
j
-
5lk |
|
is the equation of planes that all intersect at the given line
and the normal vectors of which are perpendicular to the direction vector
s
of the line.
|
|
|
|
As the plane to be found should be parallel with the
y-axis, then the normal vector
of the sheaf Ns
must be perpendicular to the unit vector
j of the
y-axis that is, the scalar product of the normal vector of the plane
and the unit vector
j
must be zero, thus
|
|
Ns
^
j
=>
Ns
·
j = 0.
|
|
Since a scalar product of two vectors expressed by their coordinates is
|
|
a · b = axbx +
ayby + azbz
and since j
= 0 · i + 1 ·
j + 0 · k
|
|
then,
Ns
·
j = 5 · 0 + (-
3
+ 4l) · 1 + (-5l)
· 0 = 0
=>
l
= 3/4.
|
|
By plugging l
= 3/4 into (5x
-
3y -
1)
+ l(4y
-
5z + 3) = 0 obtained
is 4x
-
3z + 1 = 0 the plane through the given line that
is parallel to the
y-axis.
|
|
|
| Example:
Through the line |
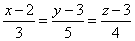 |
(the
same as in the previous example) lay a plane
|
|
| orthogonal to the
plane
4x
-
2y + z -
4 = 0 and determine its equation.
|
| Solution: Write given line as the intersection of two planes (like in
the above example) to form the equation
of a
sheaf,
|
|
5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
and Ns
= 5i + (-
3
+ 4l)
j -
5lk
|
|
that is the plane parameter l
of which should be determined so the plane to be perpendicular to the given plane.
|
|
In this case, the normal vector of the sheaf
Ns
and the normal vector of the given plane N
= 4i -
2 j + k, are
orthogonal to each other, therefore
|
|
Ns
^ N
=>
Ns
· N = 0 that
is, 5 · 4 + (-
3
+ 4l) · (-2)
+ (-5l) · 1 = 0 => l =
2.
|
|
Then, by plugging l
= 2 into 5x
+ (-
3
+ 4l) ·
y -
5lz +
(3l
-
1) = 0
|
|
obtained is 5x
+ 5y -
10z + 5 = 0
or x
+ y -
2z + 1 = 0
|
|
the equation of the plane which passes through the given line perpendicular to the given plane.
|
|
|
|
The angle between line and plane
|
|
The angle j
between a line and a plane is the angle subtended by the line and its orthogonal projection onto
the plane.
|
|
Since the normal vector
N =
Ai + Bj + Ck
of the plane forms with the direction vector s =
ai + bj + ck
of the line the angle y
= 90° -
j,
the angle j
between a line and a plane we calculate indirectly, that is
|
|
|
|
If a line is perpendicular to a
plane, its projection onto the plane is a point and
therefore its direction vector and the normal vector of the plane are collinear, i.e.,
|
|
|
| If
a line is parallel to a plane, then
|
s
^ N
=>
s
· N = 0,
j =
0°.
|
|
|
|
|
| Example:
Given is a line |
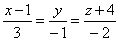 |
and
a plane x
-
3y + 2z -
8 = 0, find the angle between
|
|
| the line
and the plane.
|
| Solution: From the equations of the line and the plane,
s = 3i
-
j -
2k and N =
i -
3j + 2k
so that
|
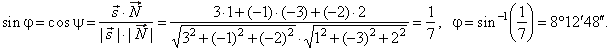
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Coordinate
geometry contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |