|
| Coordinate
geometry or Analytic geometry |
|
|
|
|
|
|
|
|
|
|
|
Points,
Lines and Planes in Three-Dimensional (3D) Space |
 Position
of two lines in a three-dimensional space
Position
of two lines in a three-dimensional space
|
|
Coplanar lines and skew lines
|
 Line and plane in a three-dimensional space
Line and plane in a three-dimensional space
|
 Two planes in a
three-dimensional space
Two planes in a
three-dimensional space
|
|
The line of intersection of two planes
|
 Orthogonality of line and plane
Orthogonality of line and plane
|
 Orthogonality of two planes
Orthogonality of two planes
|
 Orthogonal projection of a point onto a plane
Orthogonal projection of a point onto a plane
|
|
The distance from a point to a plane
|
 Angle between a line
and a plane, and angle between two planes
Angle between a line
and a plane, and angle between two planes |
|
|
|
Plane Analytic Geometry |
 Coordinate
plane, points, line segments and lines
Coordinate
plane, points, line segments and lines
|
|
The distance formula
|
|
The midpoint formula
|
 Dividing
a line segment in a given ratio
Dividing
a line segment in a given ratio |
 Area
of a triangle
Area
of a triangle |
|
The
coordinates of the centroid of a triangle |
|
|
| Position
of two lines in a three-dimensional space
|
| Exactly one line passes through two different points in a space. |
| Three points not on the same line
define a plane. |
| A plane is also
defined by: |
|
- a line and a point not on the line;
- a point and a line, which is normal/perpendicular to the plane; |
|
- two lines which intersect;
- two lines which are parallel. |
| Two lines are parallel if they
do not intersect and they are coplanar (lie on the same plane). |
| Two
lines which do not intersect but which are not coplanar are called
skew lines. |
| Skew lines do not lie in a single plane together. |
|
|
|
|
| The relations between points, lines and planes are represented by sides, edges, diagonals and vertices of the rectangular
parallelepiped (cuboid) shown in the pictures below. |
|
|
|
| Line and plane in a three-dimensional space
|
| A line l intersects a plane
P
at a point A, as shows the left picture. |
| A line is defined to be
parallel to a plane if the line and the plane are disjoint (empty
intersection). That is, there is a line in the plane which is parallel to
the given line, as shows the right picture. |
| The line
k below lies in the plane P1
and P2 . |
|
|
|
| Two planes in a
three-dimensional space
|
| Two distinct planes either are disjoint (empty intersection) or
intersect in a line. |
| Two disjoint planes are called parallel. |
|
|
|
| Orthogonality of line and plane
|
| A line is perpendicular to a plane if it is perpendicular to every line
in the plane that passes through its intersection point. |
| The plane
P2
is perpendicular to the plane P1
if there is a line in
P2
which is perpendicular to the plane
P1 . |
|
|
|
|
| Orthogonal projection of a point onto a plane
|
| Orthogonal projection of a point
P
onto a plane is the intersection point P' of the perpendicular drawn from
P
to the plane of projection. |
| Orthogonal projection of a line segment is a line segment or point
depending of the position of the line segment in relation to the plane
of projection. |
| The projection will be a point if the line segment is
perpendicular to the plane of projection. |
|
|
|
| The distance from a point to a plane is the distance from the
point to its orthogonal projection to the plane, i.e.,
AA'
=
d(A,A'). |
| For
example, if
the surface of a triangle and the plane of projection are
mutually perpendicular, as is shown in the picture below, then
the projection of the triangle is a line segment, otherwise the
projection is a triangle. |
|
|
|
| Angle between a line
and a plane, and angle between two planes |
| The
angle between a line and a plane is the angle between the line
and its orthogonal projection to the plane. |
| The
angle between two
planes is the angle between two lines, one lying in each plane, drawn perpendicular to the intersection of the planes at the same
point, as is shown below. |
|
|
|
|
Plane Analytic Geometry |
| Coordinate
plane, points, line segments and lines
|
| The distance formula
|
| The
distance between two given points in a coordinate
(Cartesian) plane. |
|
|
|
| The midpoint formula
|
| The
point on a line segment that is equidistant from its endpoints
is called the midpoint. |
|
|
|
| Dividing a line segment in a given ratio
|
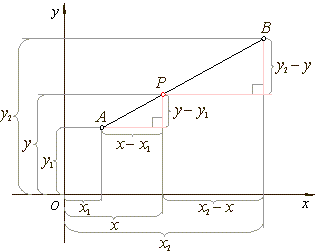
| A
given line segment AB
in a Cartesian plane can be divided by a point P
in a fixed ratio, internally or externally. |
| If
P
lies between endpoints then it divides AB
internally. If P
lies beyond the endpoints A
and B
it divides the segment AB
externally. |
| The
ratio of the directed lengths l
=
AP
:
BP |
| is
negative in the case of the internal division since the segments
AP
and BP
have opposite sense, while in the external division, the ratio l
is positive. |
 |
|
| As
l
=
AP
:
BP |
| and
shown triangles are similar, then |
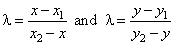 |
| which,
with l
negative, gives |
|
|
| the coordinates of
the point P. |
| |
|
|
|
| Area
of a triangle |
| The
rectangular coordinates of three points in a coordinate plane
describe a triangle. Using given coordinates we derive the
formula for the area of the triangle, as is shown in the diagram
below. |
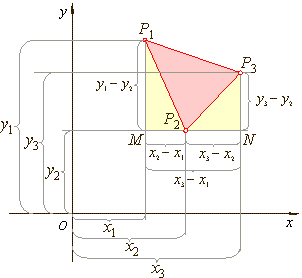 |
| The
area of the given triangle P1P2P3
equals |
| the
area of the trapezium P1MNP3
minus
the |
| sum
of the areas of the right triangles, P1MP2
and |
| P2NP3,
that is |
| PD =
1/2·[(y1 -
y2)
+ (y3 -
y2)]
· (x3 -
x1)
- |
| -
1/2·[(y1
- y2)·(x2
- x1)
+ (y3 -
y2)·(x3
- x2)] |
| which
after simplifying and rearranging gives |
| PD=1/2·[x1(y2
- y3)
+ x2(y3 -
y1)
+ x3(y1 -
y2)] |
|
|
|
| The
coordinates of the centroid of a triangle |
| The
point of coincidence of the medians of a triangle is called the
centroid. |
| The
median is a straight line joining one vertex of a triangle to
the midpoint of the opposite side and divides the triangle into
two equal areas. |
| The
centroid cuts every median in the ratio 2
: 1 from a vertex to the
midpoint of the opposite side. |
| The
coordinates of the centroid of a triangle given its three
points, P1, P2 and
P3
in a coordinate plane: |
| The
centroid M(x,
y),
where |
x
= (x1 + x2
+ x3) / 3,
y = (y1
+ y2
+ y3)
/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Coordinate
geometry contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |