|
| Solid
Geometry |
|
|
|
| |
|
Prisms |
 Cube
Cube
|
 Rectangular prism
or rectangular parallelepiped
(cuboid)
Rectangular prism
or rectangular parallelepiped
(cuboid)
|
 Right triangular prism
Right triangular prism
|
 Regular right triangular prism
Regular right triangular prism
|
 Regular right hexagonal prism
Regular right hexagonal prism
|
|
|
|
|
|
|
| Prism |
| A
prism is a polyhedron (having five or more faces) with two parallel and congruent polygonal bases, so
that all cross-sections taken parallel to the bases are also congruent with the
bases, thus all lateral faces (sides) are parallelograms. |
| Lateral
faces meet in line segments called lateral
edges. |
| A
right prism is one whose lateral
faces and lateral edges are perpendicular to its bases. The
lateral faces of a right prism are all rectangles, and the
height of a right prism is equal to the length of its lateral
edge. |
| A
regular prism has regular polygons as bases. A regular
polygon is one that has all sides equal in length and all angles
equal in measure. |
| Thus,
a right regular prism is one with
regular polygon bases and perpendicular rectangular lateral
sides. |
|
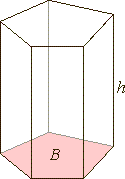 |
| S
= 2B + Slat |
-
surface of a prism |
|
Slat = P ·
h |
-
lateral surface |
| V
= B · h |
- volume
of a prism |
| B
-area of
base, P
- perimeter of base, h
-height
of a prism |
|
|
|
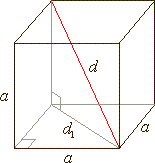
| Cube
|
| A
solid with six identical square faces that are mutually
perpendicular. |
|
 |
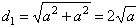 |
|
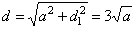 |
- diagonal |
| S
= 2B + Slat
= 2a2
+
4a2
= 6a2 |
-
surface |
| V
= B · h = a2
· a = a3 |
- volume |
|
|
|
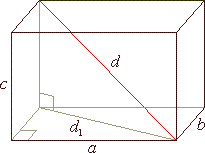
| Rectangular prism or
rectangular parallelepiped (cuboid)
|
| A
solid of which the six faces are mutually perpendicular
rectangles is called a rectangular parallelepiped or
a rectangular prism.
|
|
 |
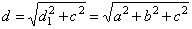 |
- diagonal |
| S
= 2B + Slat
= 2(ab + ac + bc) |
-
surface |
| V
= B · h = a
· b · c |
-
volume |
|
|
|
| Right triangular prism
|
| A
right triangular prism is made of two triangular bases and three
rectangular faces with lateral edges perpendicular to the bases. |
|
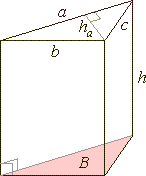 |
| S
= 2B + Slat
= a
ha + (a + b
+ c)· h |
-
surface |
| V
= B · h = 1/2 ·
a
ha · h |
-
volume |
|
|
|
| Regular right triangular prism
|
| A
prism made of two equilateral triangular bases and three
identical rectangular sides is called a regular right triangular
prism. |
|
|
|
|
| Regular right hexagonal prism
|
| A prism made of two regular hexagonal bases and six identical rectangular sides is called a regular right hexagonal prism. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |