|
Integrating
irrational functions
|
| Integration of
irrational functions of the form |
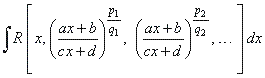 |
|
| where,
R
is a rational function and, p1,
q1,
p2,
q2,
. . . are integers, we
can solve |
| using substitution |
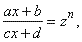 |
where
the power n
is the least common multiple of q1,
q2,
. . . .
|
|
|
|
Integration of
irrational functions examples
|
| Example:
Evaluate |
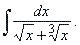 |
|
|
|
|
| Example:
Evaluate |
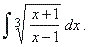 |
|
|
|
|
| Integration of
irrational functions of the form |
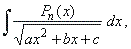 |
|
| where
Pn(x)
is an n-th
degree polynomial. |
| Set |
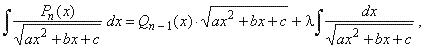 |
|
| where
Qn -
1(x) is an (n
-
1) -th
degree polynomial of undetermined
coefficients and l
is a constant.
|
| Coefficients
of the polynomial Q
and the constant l
we obtain by deriving the above identity. |
|
|
|
|
Solution:
|
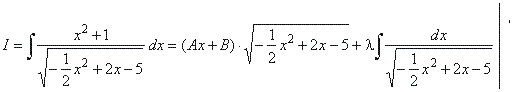 |
|
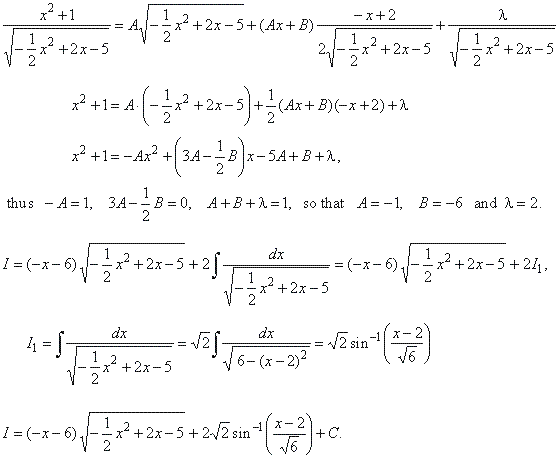
|
|
| Example:
Evaluate |
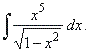 |
|
|
Solution:
|
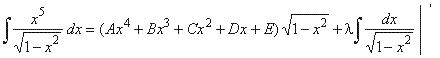 |
|
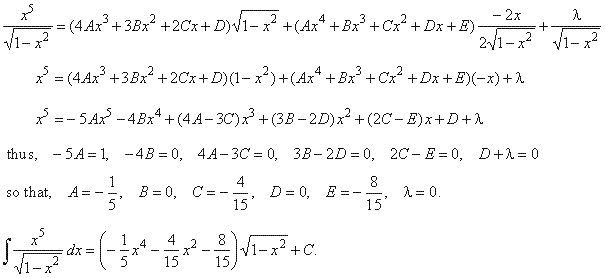
|
|
| Integration of
irrational functions of the form |
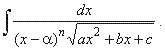 |
|
|
Given
integral can be solved using the substitution
x
-
a
= 1 / t.
|
|
| Example:
Evaluate |
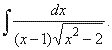 |
|
|
|
|