|
|
|
|
Integral
calculus
|
|
|
|
Integrating
rational functions
|
|
The
Ostrogradsky method of the integration of a proper rational
functions
|
|
The
integration of a rational fraction whose denominator Q (x)
has multiple or repeated roots.
|
| If
P (x)
and Q (x)
are polynomials with real coefficients and P (x)
/ Q (x)
is a proper fraction, and Q (x)
has multiple
roots, then
|
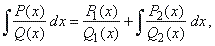 |
| where
Q1(x)
is the greatest common divisor of Q (x)
and its derivative Q'
(x),
while |
| Q2(x)
= Q (x) / Q1(x).
|
| Undetermined
coefficients of he polynomials P1(x)
and P2(x),
whose
degrees are one less than of the polynomials
Q1(x)
and Q2(x)
respectively, we calculate by deriving the above integral
identity.
|
|
|
The
Ostrogradsky method of the integration of a proper rational
functions examples
|
| Example:
Evaluate |
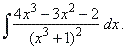 |
|
|
Since
Q(x)
= (x3 + 1)2
and Q'
(x) = 6x2(x3 + 1)
then Q1(x)
= x3 + 1
is |
| the greatest common divisor of
Q(x)
and Q'
(x),
and Q2(x)
= Q (x) / Q1(x)
= x3 + 1.
Therefore,
|
| Solution: |
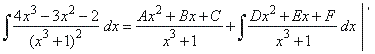 |
|
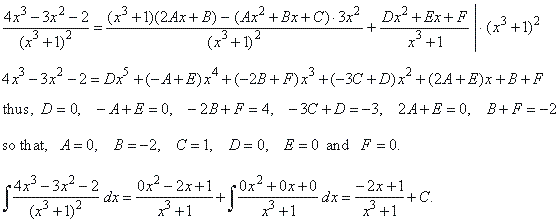
|
|
| Example:
Evaluate |
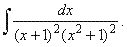 |
|
|
Since
Q(x)
= (x + 1)2 · (x2 + 1)2
and Q'
(x) = 2(x + 1)
· (x2 + 1)2
+
4x(x + 1)2
· (x2 + 1)
or
|
|
Q'
(x) = 2(x + 1)(x2 + 1)[(x2 + 1)
+ 2x(x + 1)]
then Q1(x)
= (x + 1) (x2 + 1) and |
|
Q2(x)
= Q (x) / Q1(x)
= (x + 1) (x2 + 1).
Therefore,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
M
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|