|
|
|
|
Analytic geometry
- Conic sections
|
|
|
|
Parabola
and line
|
|
Common points of a line and a parabola
|
Common points of a line and a parabola we determine by solving their equations as the system of two
equations in two unknowns, |
|
(1)
y = mx
+ c
(1)
=> (2) m2x2
+ 2(mc
-
p)x + c2
=
0, |
|
(2)
y2 =
2px therefore,
the coordinates of intersections of a line and a parabola |
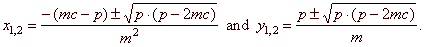 |
|
|
Condition for a line to be the tangent to the parabola
- tangency condition
|
|
In the formulas for calculating coordinates of intersections there is the expression under the square root
whose value determines three possible cases regarding mutual position of a line and a parabola, |
|
thus for p >
0 and, |
|
p
-
2mc >
0
- the line intersects the parabola at two points S1(x1, y1) and S2(x2, y2), |
|
p
-
2mc
< 0 - the
line and the parabola do not intersect. |
|
p
-
2mc
= 0 - the line is the
tangent of the parabola and have one point of contact |
|
D((p
-
mc)/m2,
p/m)) or by substituting
p
= 2mc,
the
tangency point D(c/m,
2c), |
| If we write the above conditions as |
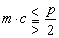 |
then these
three cases can be explained graphically as |
|
|
the relation between parameters m
and c
of the line and the position of the focus F(p/2,
0).
|
| At the y-intercept
N
of the line drawn is a perpendicular which intersects the x-axis at
M,
then |
| ON
= | c | and OM
= | c · tan
a
|
= | m · c |.
|
| Therefore, when the point
M
is located;
|
| - to the left of
F, i.e.,
if m
· c
< p/2
|
|
the line intersects the parabola at
S1and S2,
|
| - to the right
of F, i.e.,
if m
· c >
p/2
|
|
the line and the parabola do not intersect,
|
| - at the focus F
or if m
· c
= p/2
|
|
the line is the tangent of the parabola.
|
|
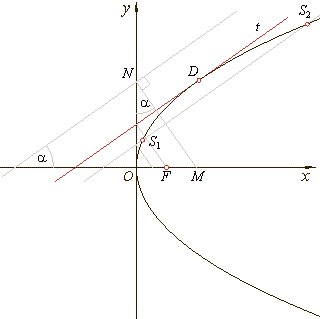 |
|
|
|
The equation of the tangent and the normal at the point on the parabola
|
|
|
|
Properties of the parabola
|
|
:: Using equations of the tangent and normal expressed by coordinates of the tangency
point and
the figure above;
|
|
a) y-intercept
ct
of the tangent equals half of the ordinates of the tangency point, ct
= y1/2. |
|
b) the projection
AB
of the segment BP1
of the tangent to the x-axis, i.e., to the axis of the parabola,
is equal to twice the abscissa of the tangency
point, so |
| AB
= St
= 2x1 - the line segment
AB
is called the subtangent. |
|
c) the projection
AC
of the segment CP1
of the normal to the x-axis is equal to the parameter
p, i.e., |
| AC
= Sn
= p - the line segment
AC
is called the subnormal. |
|
As points B
and C
are x-intercepts of the tangent and the normal their abscissas we determine by solving corresponding equations for y =
0, so |
| put y =
0 into equation of the tangent, |
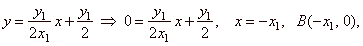 |
|
| put
y =
0 into equation of the normal, |
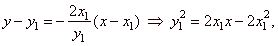 |
|
|
|
|
Thus, the focus
F(p/2,
0) bisects the line segment
BC
whose endpoints are x-intercepts of the tangent and
the normal, as shows the figure above. |
|
| ::
The tangent at any point on the parabola bisects the angle
j between focal distance and the perpendicular
to the directrix and is equally inclined to the focal distance and the axis of the parabola. |
|
The normal at the tangency
point bisect the supplementary angle of the angle
j.
|
|
Since,
DP1
= FP1
= r
= x1
+ p/2,
|
|
and
BF
= FC
= x1
+ p/2
= r, and DP1
|| BC
|
| then, following triangles are
congruent,
|
| DBFD
@
DFCP1
@
DFP1D
|
|
so, the quadrangle
BFP1D
is the rhombus and its
diagonal BP1
bisects the angle j.
|
|
This property is known as the reflective property of the parabola.
|
| A light rays coming in parallel to the axis of a
parabolic mirror (telescope), are reflected so that they all
pass through the focus. Similarly, rays originating at the focus (headlight) will be reflected parallel to the axis.
|
|
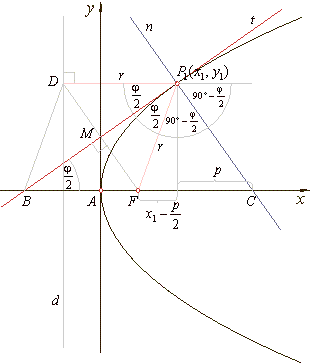 |
|
|
|
::
Tangents drawn at the endpoints of a focal chord intersect at right angles on the
directrix. |
|
a)
Solving the system of equations of tangents,
|
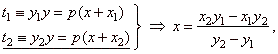 |
| x
is the abscissa of the intersection S
of tangents.
|
|
The slope of the focal chord line through
tangency points,
|
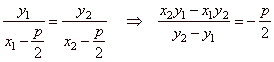 |
|
therefore,
x = -
p/2 is the abscissa
of the intersection S(-
p/2, y) and the equation of the directrix
d.
|
|
b)
The tangent to the parabola which passes through intersection
S, which
lies on the directrix, must satisfy tangency condition, |
|
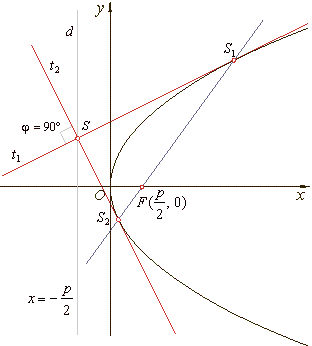 |
|
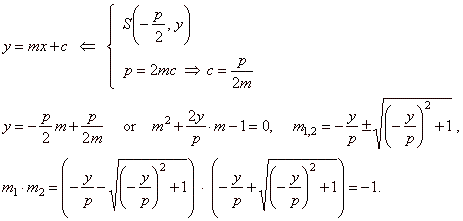 |
| Thus, satisfied is condition for
perpendicularity, m1
· m2
=
-
1 =>
j
=
90°. |
|
|
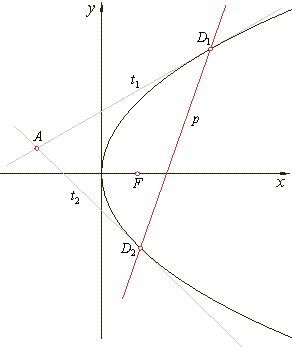
Polar of the parabola
|
| The polar
p
of a point A(x0, y0), exterior to the parabola
y2 = 2px, is the secant through the contact
points of the
tangents drawn from the point A
to the parabola. |
|
The tangency points
D1(x1, y1)
and D2(x2, y2)
and the point A
satisfy the equations of tangents,
|
|
t1::
y1y0
= p(x0
+ x1) and
t2
:: y2y0
= p(x0
+ x2).
|
|
Subtracting
t2
-
t1,
|
| y0(y2
-
y1)
= p[(x0
+ x2)
- (x0
+ x1)]
|
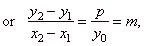 |
|
obtained is the slope of the polar. By plugging the slope into equation of the line through the given point
|
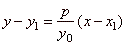 |
or
y0y
= y1y0
+ px -
px1 |
|
|
since y1y0
= p(x0
+ x1),
|
| then
y0y
= p(x
+ x0)
the
equation of the
polar.
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
D
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|