34
 
Analytic geometry - Conic sections
 Parabola
 Definition and construction of the parabola

  By intersecting either of the two right circular conical surfaces (nappes) with the plane parallel to any generator of the cones, then the intersection curve is the parabola.
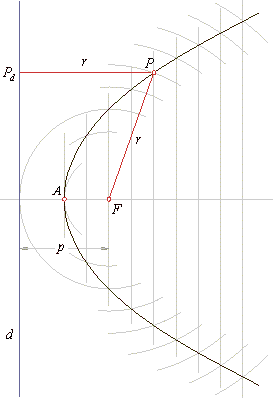
A parabola is the set of all points in a plane that are the same distance from a point F, called the focus, and a line d, called the directrix.

A parabola is uniquely determined by the distance of the focus from the directrix.

This distance is called the focal parameter p and its midpoint A is the vertex (apex) of the parabola.

The parabola has an axis of symmetry which passes through the focus perpendicular to the directrix.

The distance of any point P of the parabola from the directrix and from the focus is denoted r, so

d(Pd P) = FP = r.
Construction of the parabola

To a given parameter p of the parabola draw corresponding directrix d and the focus F.

To the distances greater then p/2 draw lines, of arbitrary dense, parallel to the directrix.

Then, intersect each line at two symmetric points by arc centered at the focus with a radius which equals the distance of that line from the directrix.

The distance p/2 from the vertex A to the directrix or focus is called focal distance.

 Vertex form of the equation of a parabola

If a parabola is placed so that its vertex coincides with the origin of the coordinate system and its axis lies along the x-axis then for every point of the parabola
According to definition of the parabola
FP = d(Pd P) = r  or
after squaring
or y2 = 2px the vertex form of equation of the parabola,

or  y2 = 4ax  if the distance between the directrix and focus is given by  p = 2a.

The explicit form of the equation  y = ± Ö2px

shows that to every positive value of x correspond two opposite values of y which are symmetric relative to the x-axis.

The parabola   y2 = 2px,  p > 0
is not defined for x < 0, it opens to the right.
For x = p/2 the corresponding ordinate y = ± p.
This parabola is not a function since the vertical line crosses the graph more than once.
A focal chord is a line segment passing through the focus with endpoints on the curve.
The latus rectum is the focal chord (P1P2 = 2p) perpendicular to the axis of the parabola.
Therefore, we can easily sketch the graph of the parabola using following points,
A(0, 0), P1,2(p/2, ± p) and P3,4(2p, ±2p)
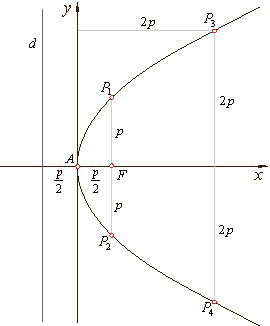Transformation of the equation of a parabola

The equation  y2 = 2px,  p < 0  represents the parabola opens to the left since must be y2 > 0. Its axis of symmetry is the x-axis.

If variables x and y change the role obtained is the parabola whose axis of symmetry is y-axis.

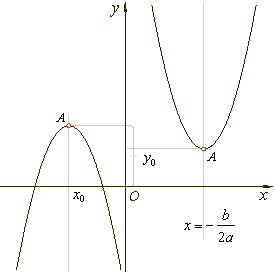
For  p > 0 the parabola opens up, if  p < 0 the parabola opens down as shows the below figure.

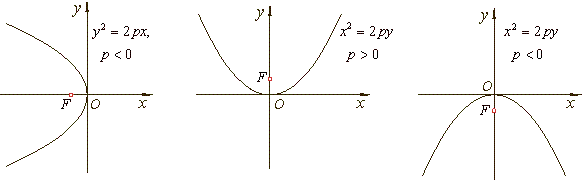This parabola we often write  y = ax2, where a = 1/(2p) , with the focus at F(0, 1/(4a)) and the directrix y = -1/(4a). This parabola is a function since a vertical line crosses its graph at only one point.

Equation of a translated parabola - the standard form

By parallel shifting of the parabola  y2 = 2px in the direction of the coordinate axes the vertex of the parabola can be brought at a point A(x0, y0) while coordinates x and y of every point of the parabola

changes by the value of the translations x0 and y0, so that equation of the translated parabola is

(y - y0)2 = 2p(x - x0)

If p > 0 the parabola opens to the right and if  p < 0 the parabola opens to the left.

If the focal parameter p = 2a then the above equation

becomes,        (y - y0)2 = 4a(x - x0).

The translated parabola with the axis parallel to the x-axis can also be written as

x = ay2 + by + c.
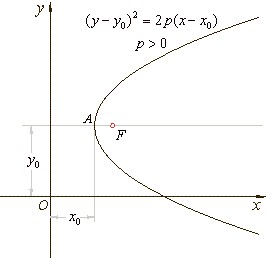The parabola whose axis of symmetry is parallel to the y-axis
By translating the parabola  x2 = 2py  its vertex is moved  from the origin to the point A(x0, y0) so that its equation transforms to
  (x - x0)2 = 2p(y - y0).

The axis of symmetry of this parabola is parallel to the y-axis. This parabola is a function that we usually write

y = ax2 + bx + c   or   y - y0 = a(x - x0)2,
where
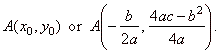This parabola opens up
if a > 0  and opens down if a < 0.
Equations of the parabola written in the general form
a) the axis of the parabola parallel to the x-axis b) the axis of the parabola parallel to the y-axis
Ay2 + Bx + Cy + D = 0,  A and B are not zero, Ax2 + Bx + Cy + D = 0,  A and C are not zero
or   x = ay2 + by + c,  a is not zero. or   y = ax2 + bx + c,  a is not zero.
Note that the parabola has equation that contains only one squared term.
Parametric equations of the parabola

Parametric equations of the parabola y2 = 4ax with the vertex A at the origin and the focus F(a, 0), and of its translation (y - y0)2 = 4a(x - x0) with the vertex A(x0, y0) and the focus F(x0 + a, y0) written
respectively are,

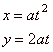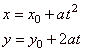Parametric equations of the parabola x2 = 4ay with the vertex A at the origin and the focus F(0, a), and of its translation (x - x0)2 = 4a(y - y0) with the vertex A(x0, y0) and the focus F(y0, y0 + a) written 
respectively are,

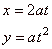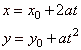Example:  Write equation of the parabola y2 = 2px passing through the point P(-4, 4) and find the focus, the equation of the directrix and draw its graph.

Solution:  The coordinates of the point P must satisfy the equation of the parabola

    P(-4, 4)   =>    y2 = 2px
                            42 = 2p(-4)   =>   p = -2

thus, the equation of the parabola   y2 = -4x.

The coordinate of the focus,

since  F(p/2, 0)  then  F(-1, 0).

The equation of the directrix, as x = - p/2,   x = 1.

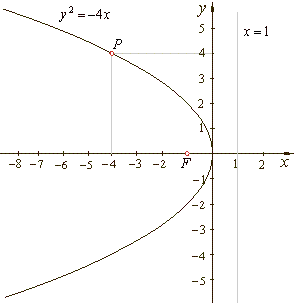Example:  Find the vertex, the focus and the equation of the directrix and draw the graph of the parabola      y = -x2 + 6x - 7.

Solution:  Rewrite the equation of the parabola in the translatable form

(x - x0)2 = 2p(y - y0)  or   y - y0 = a(x - x0)2
so, y = -x2 + 6x - 7  =>  y = -(x2 - 6x) - 7
                                        y = -[(x - 3)2 - 9] - 7
y - y0 = a(x - x0)2,    y - 2 = -(x - 3)2,  a = -1.
The vertex of the parabola  A(x0, y0),  or  A(3, 2).
he focus  F(x0, y0 + 1/(4a)),  or  F(3, 7/4).
The equation of the directrix,
y = y0 - 1/(4a),    y = 2 + 1/4  or  y = 9/4.
 
 
 
 
 
 
 
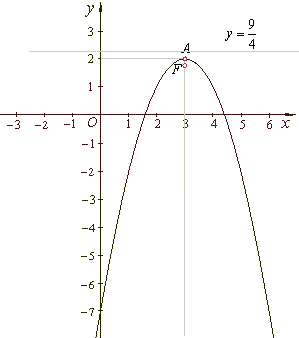Contents D
 
 
 
 
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.