|
Circle and line
|
|
::
Condition of tangency - Condition for a line to be the tangent to a circle
|
|
Condition for a line to be the tangent to the circle with center at the
origin
O(0, 0)
|
|
A line touches a circle if the distance of the center of the circle to the line is equal to the radius of the circle, i.e., if d
= r. |
|
The distance of the center
S(0,
0) of a circle
x2
+ y2 = r2
from a line y =
mx + c or -mx
+ y -
c
= 0, |
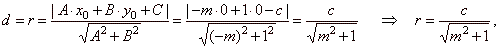 |
| and after squaring
obtained is r2·(m2
+ 1)
= c2
the condition for a line
y =
mx + c
to be a tangent to the circle x2
+ y2
= r2. |
|
|
Condition for a line to be the tangent to the translated circle (x
-
p)2 + (y -
q)2 = r2
|
| In this case, the distance
d
of the center
S(p,
q) of the circle to a line
-mx
+ y -
c
= 0 or
y =
mx + c,
must be equal to the radius r
of the circle, thus |
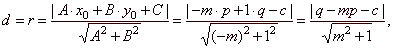 |
| after squaring
obtained is r2·(m2
+ 1)
= (q -m
p -
c)2 |
| the condition for a line
y =
mx + c
to be a tangent
to a translated circle with the center at S(p,
q). |
|
|
Example:
Given is a line
-3x +
y + 1 = 0 and a circle
x2
+ y2 -
6x
- 4y
+ 3 = 0,
find equations of tangents to the circle which are perpendicular to the line.
|
|
Solution: Slopes of tangents are
defined by condition of
perpendicularity, therefore |
| y =
3x -
1,
m =
3
so that
mt =
-1/3 |
| x2
+ y2 -6x
-4 y
+ 3 = 0
or
(x
-
3)2 + (y -
2)2 = 10 |
| thus,
S(3,
2)
and
r2
= 10. |
| To
find intersections c
we use the tangency condition, |
| r2·(m2
+ 1)
= (q -m
p -
c)2 |
| therefore,
10[(-1/3)2
+ 1]
= [2 -(-1/3)·3
-
c]2 |
| or
(3
-
c)
= ± 10/3
then, c1
= -1/3
and c2
= 19/3. |
| The equations of
tangents are, |
| t1
::
y =
-(1/3)x
-1/3 and t2
::
y =
-(1/3)x
+19/3. |
|
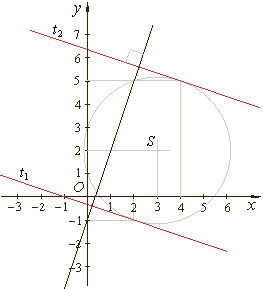 |
|
|
|
Angle between a line and a circle
|
|
The angle between a line and a circle is the angle formed by the line and the tangent to the circle at the
intersection point of the circle and the given line.
|
|
Example:
Find the angle between a line
2x +
3y -
1 = 0 and a circle
x2
+ y2 +
4x
+ 2y - 15
= 0.
|
|
Solution: Coordinates of
intersections of the line and the circle calculate by solving the system, |
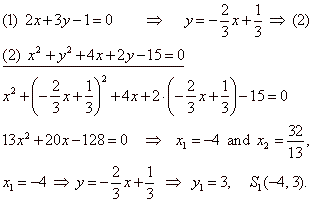 |
| Rewrite
the equation of the circle to standard form, |
| x2
+ y2 +
4x
+ 2y - 15
= 0, (x
-
p)2 + (y -
q)2 = r2 |
| thus,
(x +
2)2 + (y + 1)2 = 20,
S(-2,
-1) and
r2
= 20. |
|
 |
|
| Equation of the tangent at the intersection
S1, |
| S1(-4,
3)
=>
(x1 -
p) ·
(x -
p) + (y1 -
q) ·
(y -
q) = r2
|
| (-4
+
2)
· (x +
2)
+ (3 + 1)
·
(y
+
1)
= 20
=>
t
::
-
x
+ 2y
-
10
= 0
or y =
1/2x + 5 |
| The angle between the line and the circle is the angle formed by the line and the tangent to the circle at the
intersection point, therefore
|
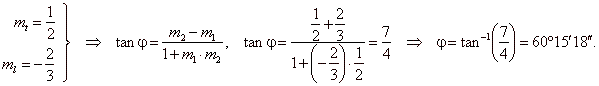 |
|
|
::
Mutual position of two circles
|
| Two circles
k1
and k2
intersect if the distance between their centers is less than the sum, but greater than difference, of their radii. |
| The coordinates of the intersection points of two circles
we calculate by solving their equations as system of two quadratic
equations, |
| k1
::
(x
-
p1)2 + (y -
q1)2 -
r12 = 0
and k2
::
(x
-
p2)2 + (y -
q2)2 -
r22 = 0. |
|
|
The radical line or the radical axis
|
| Subtracting the second equation
from the first gives equation of the line k1-
k2
= 0 through the |
| intersection
points A and
B of the circles. |
|
Coordinates of intersections
A
and B satisfy equations of
circles
k1
and k2 and
the equation of the line k1-
k2
= 0. |
| This line is called the
radical line and represents the
locus or set of all points in the plane of equal power
with respect to two non-concentric circles. |
|
The radical line
is a line perpendicular to the line connecting centers of
the two circles. |
|
Since
the slope of the line S1S2, |
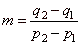 |
|
| then |
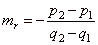 |
is
the slope of the radical line. |
|
|
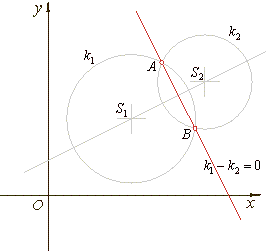 |
|
| If two circles touch each other outside then, the radical line
is at the same time their common tangent. |
|
|
The pole and the polar
|
|
Given is a circle
k
::
x2
+ y2
= r2 and a point
P(x0,
y0) outside the circle. The contact
points of tangents from P
to the circle, are at the same time the intersections of
the given circle k and the circle
k' whose center is the midpoint of the line
segment OP,
that is
|
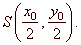 |
| Therefore, the equation of the circle
k'
is
|
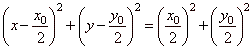 |
| or, after squaring and reducing
|
| k'
::
x2
+ y2 - x0
x
- y0
y
= 0. |
|
Equation of the line through tangency points, which
is perpendicular to the line OP, is
|
| p
::
k
- k'
= 0
or x0
x
+ y0
y
= r2. |
|
This line is called the
polar
of the
point P
with respect to the circle, and point P
is called the
pole of the polar.
|
|
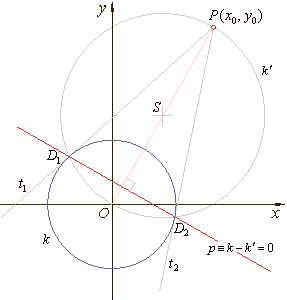 |
|
|
If given is a translated circle
(x
-
p)2 + (y -
q)2 = r2
with the center at the point
S(p,
q), then the equation of the polar of the point P(x0,
y0) is, |
| (x0 -
p) ·
(x -
p) + (y0 -
q) ·
(y -
q) = r2. |
|
|
Angle between two circles
|
Angle between two circles is defined as the angle between the two tangent lines at any of the intersection
points of the circles.
|
|
Example:
From the point
A(2,
-2)
drawn are tangents to the circle
(x +
3)2 + (y -1)2 =
17, find equations of
tangents using the polar and taking the point A
as the pole.
|
|
Solution: Coordinates of the point A
plug into equation of the polar, |
| as,
P(x0,
y0)
or
A(2,
-2),
S(-3,
1)
and
r2
= 17 |
| (x0 -
p) ·
(x -
p) + (y0 -
q) ·
(y -
q) = r2 |
| (2 +
3)
·
(x +
3) + (-2 -
1) ·
(y -
1) =
17, |
| which
gives, |
| p
::
5x
-
3y
+ 1
= 0 -
the equation of the polar. |
|
By solving system of equations of the polar and the circle
we calculate coordinates of points of contact, |
|
(1) 5x
-
3y
+ 1
= 0 |
|
(2) (x +
3)2 + (y -1)2 =
17 |
| it
follows that, D1(1,
2) and
D2(-2,
-3). |
|
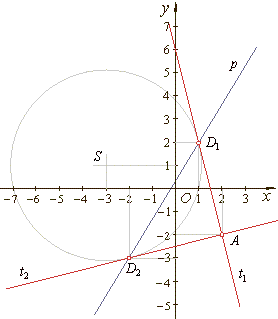 |
|
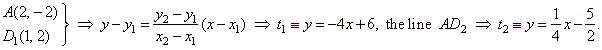 |
|