|
|
|
|
Analytic geometry
- Conic sections
|
|
|
|
Conics,
a family of similarly shaped curves
|
|
::
Circle
|
|
By intersecting
either of the two right circular conical surfaces (nappes) with the plane perpendicular to the
axis of
the cone the resulting intersection is a circle.
|
|
General equation of a circle with the center
S(p, q)
- translated circle
|
|
A circle with the center
at the point S(p,
q) and radius r is a set of all points P(x,
y) of a plane to whom
|
| the
distance from the center,
SP
= r
or |
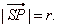
|
|
|
|
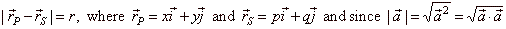 |
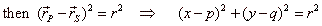 |
| is
the general equation
of a circle with the
center S(p,
q). |
|
| Equation of the circle with the
center at the origin
O(0,
0),
|
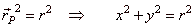 |
|
|
Example:
A circle passes through points A(2, 4) and
B(-2, 6) and its center lies on a line
x + 3y
-
8 = 0. Find equation of the circle.
|
|
|
|
Circle through three points
|
|
A circle is uniquely determined by three points not lying on the same line. If given are points,
A,
B
and C
then the intersection of any pair of the perpendicular bisectors of the
sides of the triangle ABC is the center of the circle.
|
|
Since all three points lie on the circle, their coordinates must
satisfy equation of the circle
|
| (x
-
p)2 + (y -
q)2 = r2. |
|
Thus, we obtain the system of three equations in three unknowns
p,
q
and r.
|
|
Subtracting second equation from first and then third from first
we obtain two equations in two unknowns p and
q.
|
|
Solutions of that system plug into any of three equations to
get r.
|
|
 |
|
|
|
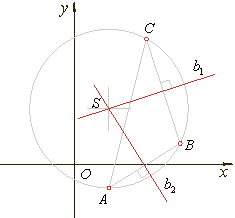
Example:
Find equation of a circle passing through three
points, A(-2,
-6),
B(5, -7)
and C(6, 0).
|
|
Solution: The coordinates of the points, A,
B
and C
plug into equation (x
-
p)2 + (y -
q)2 = r2,
|
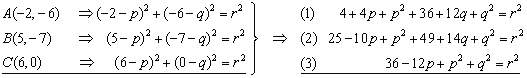 |
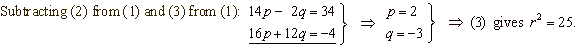 |
| Thus,
the equation of the circle through points A,
B
and C,
(x
-
2)2 + (y +
3)2 = 25. |
|
|
::
Circle
and Line
|
|
Line circle intersection
|
|
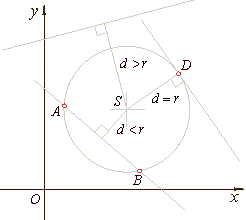
A
line and a circle in a plane can have one of the three positions in relation
to each other, depending on the distance d
of the center S(p,
q) of
the circle
|
| (x
-
p)2 + (y -
q)2 = r2
from
the line Ax
+ By + C = 0, |
| where the formula for the distance: |
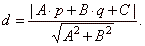 |
| If the distance of the center of a circle from a line is such that: |
|
d
< r,
then the line intersects the circle in two points, |
|
d
= r,
the line touches the circle at only one point, |
|
d
> r,
the line does not intersect the circle, and they have no common points. |
|
 |
|
|
|
Example:
At which points the line
x +
5y + 16 = 0
intersects the circle x2
+ y2 -
4x + 2y -
8 = 0.
|
|
Solution: To find coordinates of points at which the line intersects the circle solve the system of
equations
|
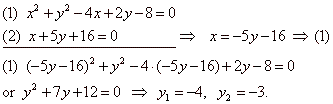 |
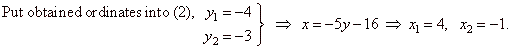 |
| So, the line intersects the circle at points,
A(4, -4)
and B(-1,
-3). |
|
|
Equation of a tangent at a point of a circle with the center at the
origin
|
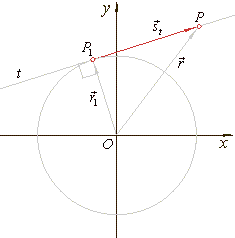
| The direction vector of the tangent at the point P1
of a circle and the radius vector of P1
are perpendicular to each other so their scalar product is zero. Points,
O,
P1
and P
in the right figure, determine vectors, |
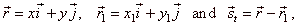 |
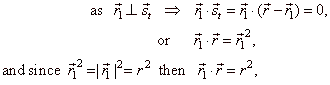 |
| the
scalar product written in
the components gives,
|
| x1x
+ y1y = r2
|
| This is
equation of a tangent at the point P1(x1,
y1)
of a circle with the center at the origin. |
|
 |
|
|
|
Equation of a tangent at a point
of a translated circle (x
-
p)2 + (y -
q)2 = r2
|
| The direction vector of the tangent at the point P1(x1, y1), of a circle whose center is at the point
S(p,
q), and the direction vector of the normal, are perpendicular, so their scalar product is zero. |
| Points,
O,
S,
P1
and P
in the right figure, define vectors, |
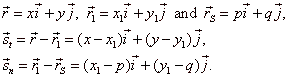 |
| Since |
 |
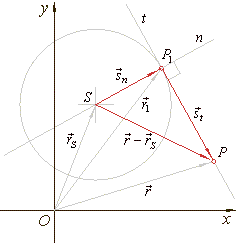
their scalar product is zero, that is |
|
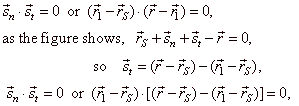 |
|
 |
|
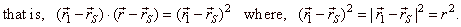 |
| Therefore, |
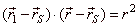 |
is
vector equation of a tangent at the point of a translated
circle, |
|
| or,
when this scalar product is written in the component form, |
| (x1
-
p) · (x
-
p) + (y1
-
q)
· (y
-
q) = r2 |
|
it
represents the equation of the tangent at the point P1
(x1, y1), of a circle whose center is at
S(p,
q).
|
|
|
Example:
Find the angle formed by tangents drawn at points of intersection of a line
x -
y + 2 = 0 and
the circle x2
+ y2 = 10.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents C
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|