|
|
|
|
Coordinate geometry
(or Analytic geometry) in three-dimensional space
|
|
|
|
::
The line of intersection of two planes
|
|
Two planes are either parallel or they intersect in a line. If planes are parallel, their coefficients of coordinates
x,
y
and z
are proportional, that is
|
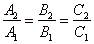 |
|
and then, the vector product of their normal vectors is zero
|
| N1
´
N2
= 0. |
|
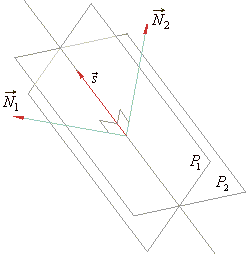
When two planes intersect, the vector product of their normal
vectors equals the direction vector s
of their line of intersection,
|
| N1
´
N2
= s. |
|
To write the equation of a line of intersection of two
planes we still need any point of that line. |
|
 |
|
|
We
can use the intersection point of the line of intersection of two planes
with any of coordinate planes (xy,
xz or
yz plane)
as that point.
|
|
|
Example:
Given are planes, P1
::
-3x
+ 2y -
3z -
1 = 0 and P2
::
2x -
y -
4z + 2 = 0, find the line of
intersection of the two planes.
|
|
Solution: Since
the equation of the plane and its normal, |
| Ax + By
+ Cz + D = 0
and N =
Ai + Bj + Ck
then, N1
= -3i
+ 2j -
3k and N2
= 2i -
j -
4k, |
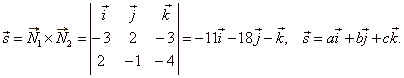 |
| To write the equation of the line of intersection, i.e., |
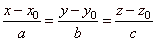 |
|
| we still need the coordinates
of any of its point P(x0,
y0, z0). |
| Let this point be the intersection of the intersection line and the
xy
coordinate plane. |
|
Then, coordinates of the
point of intersection (x,
y, 0) must satisfy equations of the given planes. |
| Therefore,
by plugging z = 0
into P1
and P2
we get, |
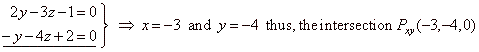 |
| so,
the line of intersection is |
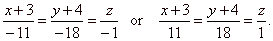 |
|
Using the same method we can check validity of obtained equation by calculating coordinates of another intersection point of the intersection line and
for example the
yz
coordinate plane, and plug them into mentioned equation. |
|
|
Projection of a line onto coordinate planes
|
| In the equation of a line, |
 |
|
| represents the orthogonal projection
of the given line onto the xy
coordinate plane. |
| At the same time, it is
spatial equation of the plane, which passes through the given line, and
is perpendicular to
the xy coordinate plane.
Similarly, |
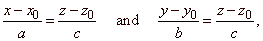 |
| represent
the equations of the projections of the given line onto the xz and the
yz coordinate
plane respectively. |
| While,
in relation to space, they are the equations
of planes passing through the given line
orthogonal to the xz and the
yz
coordinate planes respectively. |
|
|
How determine two planes of which, a given line is their
intersection line
|
| Through a given line |
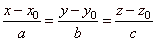 |
lay two planes each of which is orthogonal to one of the |
|
| coordinate planes. That way, given line will be determined by any of
the following pairs of
equations, |
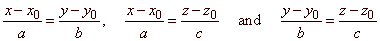 |
| as the intersection line of the corresponding planes
(each of which is perpendicular to one of the three coordinate
planes). |
|
|
Intersection point of a line and a plane
|
| The point of intersection is a common point of a line and a plane. Therefore, coordinates of intersection must
satisfy both equations, of the line and the plane. |
| The parametric equation of a line, |
| x =
x0 + at,
y = y0
+ bt and
z
= z0 + ct |
| represents coordinates of any point of
the line expressed as the function of a variable parameter t
which makes
possible to determine any point of the line according to given condition. |
| Therefore, by plugging these variable coordinates of a point of the line into
the given plane determine what value
must have the parameter t,
this point to be the common point of the line and the plane. |
|
| Example:
Given is a line |
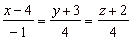 |
and a plane
4x -
13y + 23z -
45 = 0, find the |
|
| intersection
point of the line and the plane.
|
|
|
Solution: Transition from the symmetric to the parametric form
of the line
|
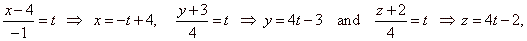 |
|
by plugging these variable coordinates
into the given plane we will find the value of the parameter t
such that these
coordinates represent common point of the line and the plane, thus |
| x =
-t +
4, y
= 4t -
3 and z
= 4t -
2 => 4x -
13y + 23z -
45 = 0 |
| which
gives, 4 · (-t +
4) - 13 · (4t -
3) + 23 · (4t -
2) -
45 = 0 Þ
t = 1. |
| Thus,
for t = 1
the point belongs to the line and the plane, so |
| x =
-t +
4 = -
1+ 4 = 3, y =
4t -
3 = 4 · 1 -
3 = 1 and z =
4t -
2 = 4 · 1 -
2 = 2. |
| Therefore, the intersection point
A(3,
1,
2) is the point which is at the same time on the line and the plane. |
|
|
Sheaf or
pencil of planes
|
| A
sheaf of planes is a family of planes having a common line of intersection.
If given are two planes |
| P1
::
A1x + B1
y
+ C1 z + D1 = 0
and P2
::
A2 x
+ B2 y + C2 z + D2
= 0 |
| of which we form
a linear system, |
| P1
+ lP2 = 0
or
(A1x + B1
y
+ C1 z + D1) + l(A2
x + B2 y + C2 z
+ D2) = 0 |
| then this expression, for every value of the parameter
l represents one plane which passes through the
common line of intersection. |
| Thus, by changing the value of the parameter
l, each time determined is another
plane of the sheaf of which, the axis of the
sheaf is the line of intersection of the given planes, P1 and
P2. |
|
For
example, to find equation of a plane of a sheaf which passes
through a given point A(x1,
y1,
z1),
plug the coordinates
of the point into the above equation of the sheaf, to determine
the parameter l
so that the plane contains
the point A. |
|
| Example:
Through a line which is written as the intersection of two planes, P1
::
x -
2y
+ 3z -
4 = 0 and
P2
::
3x + y
-
z + 1 = 0, lay a plane which passes through the point
A(-
1,
2,
1). Determine the equation of the plane. |
|
|
Solution: Write the equation of a sheaf,
P1
+ lP2 = 0
or (x - 2y
+
3z -
4)
+ l(3x +
y -
z + 1) = 0. |
| Plug
the point A
into the equation to determine l
such that the plane passes through the given point, so |
| A(-1,
2,
1)
=> P1
+ lP2 = 0
gives (-1
- 2 · 2 +
3 · 1 -
4)
+ l[3 · (-1) +
2 -
1 + 1] = 0, l =
-
6. |
| Therefore,
(x - 2y
+
3z -
4) -
6 · (3x + y -
z + 1) = 0
or -
17x -
8y
+ 9z -
10 = 0 |
| is the plane passing through
the given line and the point A. |
|
|
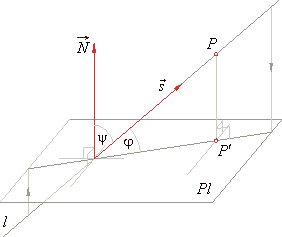
The angle between line and plane
|
| The angle j
between a line and a plane is the angle subtended by the line and its orthogonal projection onto
the plane.
|
| Since the normal vector
N =
Ai + Bj + Ck
of the plane forms with the direction vector
s =
ai + bj + ck
|
|
of the line
the angle
y
= 90° -
j,
the angle j
between a line and a plane we calculate indirectly, that is |
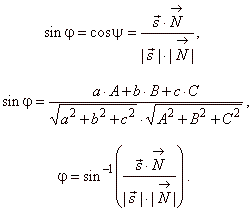 |
|
 |
|
|
If a line is perpendicular to a
plane, its projection onto the plane is a point and
therefore its direction |
| vector and the normal vector of the plane are collinear, i.e.,
s =
lN
=> j =
90°.
|
|
If
a line is parallel to a plane, then
s
^ N
=>
s
· N = 0,
j =
0°.
|
|
|
Example:
Given is a line
|
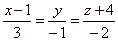 |
and
a plane x
-
3y + 2z -
8 = 0, find the angle
|
|
| between the line
and the plane.
|
|
|
Solution: From the equations of the line and the plane,
s = 3i
-
j -
2k and N =
i -
3j + 2k
so that
|
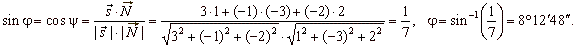 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents C
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|