Vectors, Scalar product or dot product or inner product, Scalar product in the coordinate system, Projection of a vector in the direction of another vector, the scalar and vector components

ALGEBRA

:: Scalar product or dot product or inner product

The word scalar derives from the English word "scale" for a system of ordered marks at fixed intervals used in measurement, which in turn is derived from Latin scalae - stairs.

Physical quantities like, distance, time, speed, energy, work, mass and so on, which have magnitude but no direction, are called scalar quantities or scalars. Thus, the magnitude of any vector is a scalar.

The scalar (numeric) product of two vectors geometrically is the product of the length of the first vector with projection of the second vector onto the first, and vice versa, that is



The scalar or the dot product of two vectors returns as the result scalar quantity as all three factors on the right side of the above formula are scalars (real numbers).
The result will be positive or negative depending on whether is the angle j between the two vectors are acute or obtuse.
For example, in physics mechanical work W is the dot product of force F and displacement s,
A change of the angle between the two vectors on the below picture, changes the value of the work W, from the maximal value
for j = 0° => W = \| F \| · \| s \|, to the minimal value for j = 180° => W = - \| F \| · \| s \|.

For j = 90° the force F does any work on an object, since
It is only the component of the force along the direction of motion of the object which does a work.

Perpendicularity (or orthogonality) of two vectors

Therefore, if the scalar product of two vectors, a and b is zero, i.e.,
a · b = 0 - then the two vectors are orthogonal.
And inversely, if two vectors are perpendicular, their scalar product is zero.

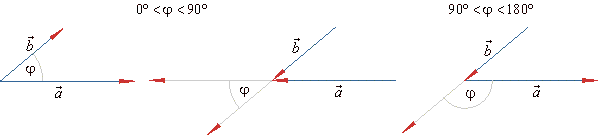
The value of the scalar product of two vectors depends on their position

Different positions of two vectors and the corresponding values of their scalar product are shown in the below figures.

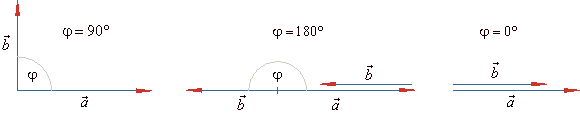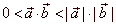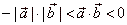Square of magnitude of a vector

The scalar product of a vector with itself, a · a = a² is the square of magnitude of a vector, that is

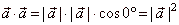thus,	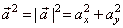- in the coordinate plane, and	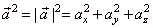- in 3D space.

Scalar product of unit vectors

The unit vectors, i, j and k, along the Cartesian coordinate axes are orthogonal and their scalar products

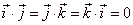and

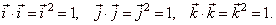Scalar or dot product properties

a) k · (a · b) = (k · a) · b = a · (k · b), k Î R

b) a · b = b · a

c) a · (b + c) = a · b + a · c

d) a · a = a² = | a |²

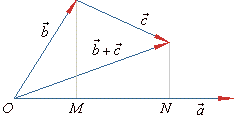According to the definition of the dot product, from the above diagram,

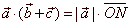then

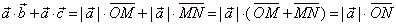what confirms the distribution law.

The associative law does not hold for the dot product of more vectors, for example

a · (b · c) is not equal (a · b) · c

since a · (b · c) is the vector a multiplied by the scalar b · c, while (a · b) · c is the vector c multiplied by the scalar a · b.

Scalar product in the coordinate system

The scalar product can be expressed in terms of the components of the vectors,

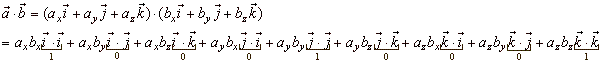thus,

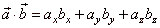- the scalar product in three-dimensional coordinate system,

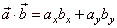- the scalar product in the coordinate plane.

Angle between vectors in a coordinate plane

From the scalar product a · b = | a | · | b | · cosj derived are, the angle between two vectors, formulas

for plane vectors

for space vectors

The cosine of the angle between two vectors, a and b represents the scalar product of their unit vectors,

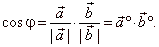
Scalar product of vectors examples

Example: Applying the scalar product, prove Thales’ theorem which states that an angle inscribed in a semicircle is a right angle.

Solution: The right figure shows that

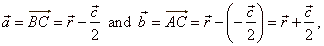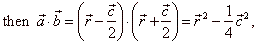since square of a vector equal to square of its length,

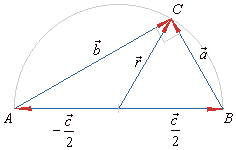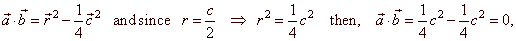therefore a and b are perpendicular vectors as a · b = 0.

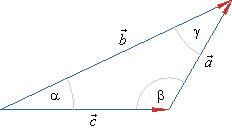
Example: Prove the law of cosines used in the trigonometry of oblique triangles.

Solution: Assuming the directions of vectors as in the right diagram

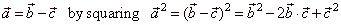Using the scalar product and substituting square of vectors
by square of their lengths, obtained is

a² = b² + c² - 2bc · cosa - the law of cosines.

In the same way,

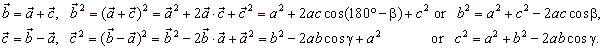Example: Determine a parameter l such that the vectors, a = -2i + l j - 4k and b = i - 6 j + 3k to be perpendicular.

Solution: Two vectors are perpendicular if their scalar product is zero, therefore

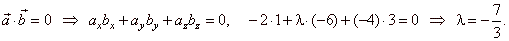:: Projection of a vector in the direction of another vector, the scalar and vector components

The scalar component

The length of projection of a in the direction of b or the scalar component a_b, from the diagram,

Thus, the scalar component of a vector a in the direction of a vector b equals the scalar product of the vector a and the unit vector b⁰ of the vector b.

The vector component

By multiplying the scalar component a_b, of a vector a in the direction of b, by the unit vector b⁰of the vector b, obtained is the vector component of a in the direction of b.

Contents B