17
 
ALGEBRA
 Vectors
 :: Vectors in a plane
Direction, length or magnitude or norm of a vector

  Physical quantities like force, velocity, acceleration or magnetic field strength, which are defined by a magnitude and a direction, are called vectors or vector quantities and are represented by directed line segment.
A vector is denoted as where the point A is

called the tail or start and point B, the head or tip.

The length or magnitude or norm of the vector a
Therefore, the length of the arrow represents the vector's magnitude, while the direction in which the arrow points, represents the vector's direction.
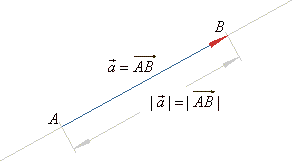A vector with no magnitude or, if the tail and the head coincide, is called the zero or null vector denoted
 Collinear, opposite and coplanar vectors
Two vectors are said to be equal if they have the same magnitude and direction or if by parallel shift or translation one could be brought into coincidence with the other, tail to tail and head to head.
Vectors are said to be collinear if they lie on the same line or on parallel lines. Two collinear vectors of the same magnitudes but opposite directions are said to be opposite vectors.

Three or more vectors are said to be coplanar if they lie on the same plane. If two of three vectors are collinear then these vectors are coplanar. Therefore, if vectors are parallel to a given plane, then they are coplanar.

 Addition of vectors
The sum of vectors, 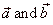can be obtained graphically by placing the tail of the  b  to the tip or head
of  a  using translation. Then, draw an arrow from the initial point (tail) of  a  to the endpoint (tip) of  b  to obtain the result.

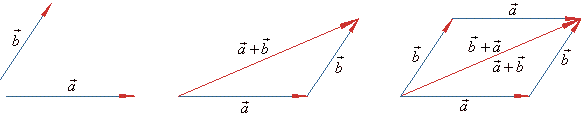The parallelogram in the above figure shows the addition  b + a  where, to the tip of  b, by translation, placed is the tail of  a  then, drawn is the resultant  b + a  by joining the tail of  b  to the tip of  a.
Note that the tips of the resultant and the second summand should coincide.
Thus, in the above figure shown is, the triangle rule (law) and the parallelogram rule for finding the resultant or the addition of the two given vectors. The result is the same vector, that is
a + b = b + a
vector addition is commutative.
Since vectors, a, b and a + b  form a triangle, they lie on the same plane, meaning they are coplanar.
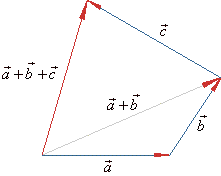
 Addition of three vectors,  a, b and c is defined as  a + b + c = (a + b) + c and represented graphically
a + b + c = (a + b) + c
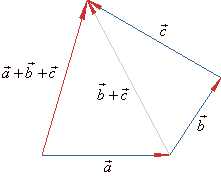
a + b + c = a + (b + c)
The above diagrams show that vector addition is associative, that is
(a + b) + c = a + (b + c)
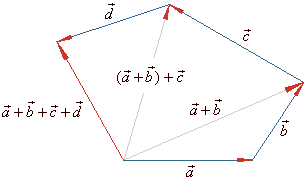
The same way defined is the sum of four vectors.
If by adding vectors obtained is a closed polygon,    then the sum is a null vector.
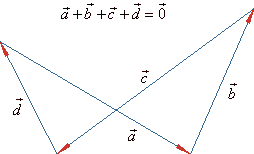By adding a vector a to its opposite vector - a, graphically it leads back to the initial point, therefore
a + (- a) = a - a = 0  thus, the result is the null vector.
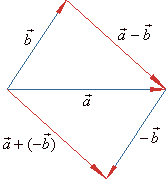
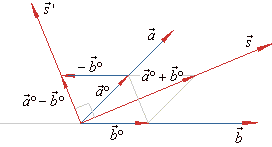
 Subtraction of vectors
Subtraction of two vectors, a and b is defined as addition of vector  a  and - b, that is
a - b = a + (- b).
As shows the right figure, subtraction of two vectors can be accomplished directly.
By using translation place tails of both vectors at the same  point and connect their tips.
Note that the arrow (tip) of the difference coincides with the tip of the first vector (minuend).
 Scalar multiplication or multiplication of a vector by scalar

Scalar is a quantity which is fully expressed by its magnitude or size like length, time, mass, etc. as any real number.

By multiplying a vector a by a real number l obtained is the vector l a  collinear to a but,
            l times longer then  a  if  | l | > 1,   or    shorter then  a  if  | l | < 1, and
                        directed as   a  if  l > 0,    or    opposite to  a  if  l < 0, as is shown in the below figure.
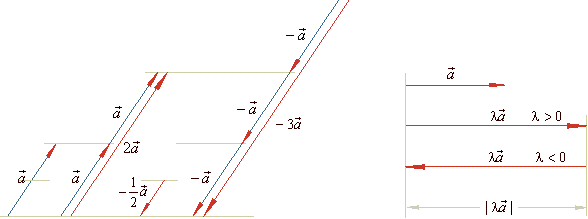Thus, the magnitude of the vector l a equals to the product of the absolute value of the real number l and the magnitude of the vector a.
For the multiplication of a vector by a real number following rules hold:
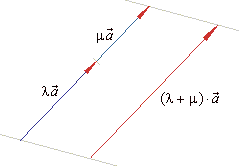
 1)   l · ( a + b ) = l a + l b
 2)   ( l + m ) · a  = l a + m a,   l, m Î R
 3)   l ( m a )  = m ( l a ) = ( m l ) a
 4)   1 · a  =  a,     -1 · a  = - a
 5)   0 · a  =  0,       m · 0  = 0
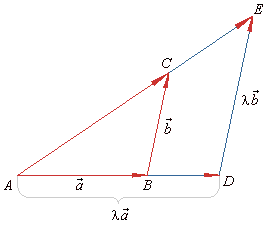
In the similar triangles ABC and ADE in the right
figure,         AE : AC = DE : BC = AD : AB = l
therefore,    AE = l ·  AC.
Since         AE = l a + l b    and    AC = a + b
then,          l a + l b = l · ( a + b ).
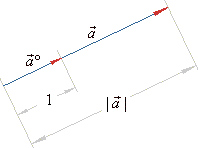
 Unit vector
A vector 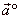is called the unit vector of a vector 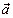if
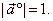Therefore,
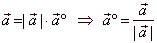the unit vector 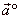determines the direction of the vector

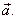Example:  Given is a regular hexagon ABCDEF with the center O. Express vectors  CD, BE, EA, and 

CE,  in terms of vectors,  AB = a  and  BC = b.
Example:  In a triangle ABC drown are medians as vectors,
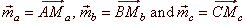Prove that
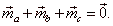Solution: Replacing the sides of the triangle by vectors directed as in the diagram,
        

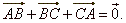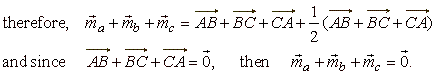
Example:  Use vectors to prove that line segments joining the midpoints of adjacent sides of a quadrangle, form a parallelogram.

Solution:  The sides of the quadrangle ABCD are replaced by vectors, directed as in the diagram so that the opposite vectors connecting midpoints are,
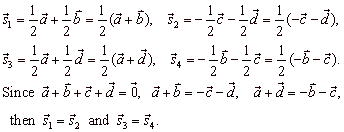As equal vectors are of same lengths and parallel, therefore the line segments connecting the midpoints of any quadrangle, form a parallelogram.

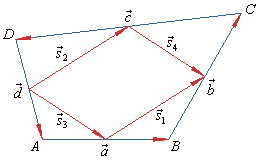
Example:  Determine a vector which coincides with the angle bisectors of vectors, a and b in the diagram.

Solution:  The unit vectors of the vectors a and b are,
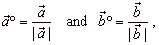and they form a rhombus whose diagonal is
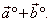That is, a vector 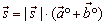will coincide with
the angle bisector, while a vector
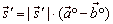defines the angle bisector of the supplementary angle of the angle between vectors, a and b.
 Linear combination of vectors

A vector  d =  l a + m b,  l, m Î R  denotes the linear combination of the vectors, shown in the left diagram.

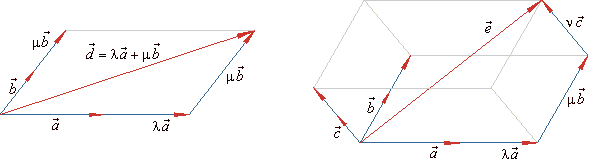On the same way, the vector  e = l a + m b + n c  represents the linear combination of the vectors, a, b and c, as shows the right diagram in the above figure.

Example:  Given is a parallelogram ABCD, the midpoint M of the side AD and the intersection point O of the diagonals. Express vectors, AO, BD, and BM  as the linear combination of vectors,  a = AB and     b = AD.

Solution:
 Linear dependence of vectors
Vectors, a = OA and b = OB whose points, O, A and B all lie on the same line are said to be linear dependent, but if the points, O, A and B do not all lie on the same line then a and b, are not collinear, and are said to be linear independent.

  a)  If a and b are linear independent vectors then every vector d of the plane determined by a and b, can be written as the linear combination of these vectors, that is in the form

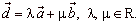Vectors, a = OA, b = OB and c = OC, whose points, O, A, B and C all lie on the same plane, are said to be coplanar or linear dependent. But if points, O, A, B and C do not all lie on the same plane, then a, b and c are not coplanar, and are said to be linear independent. 

  b)  If, a, b and c are linear independent vectors in 3D space then every vector d, from the space, can be 
represented as 
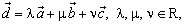that is, as the linear combination of the vectors, a, b and c.
In the below example the sides of the cuboid are replaced by three linear independent vectors, a, b and c so that the vector MN can be written as the linear combination of the vectors, a, b and c.

Example:  To a cuboid ABCDEFGH the point M divides the edge EH in the ratio EM : MH = 2 : 1 and the point N the edge AB in the ratio AN : NB = 3 : 2. Express the vector MN as the linear combination of vectors, a = AB, b = AD and c = AE.

Solution:
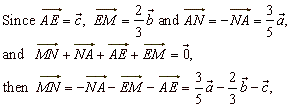MN is the linear combination of the vectors, a, b and c.
 
 
 
 
 
 
 
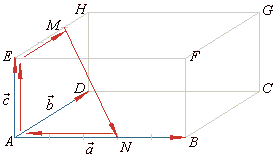Contents B
 
 
 
 
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.