|
|
|
|
ALGEBRA
|
|
|
|
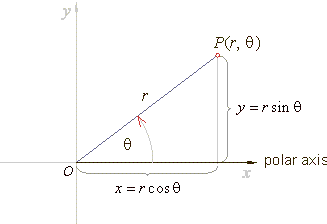
Polar coordinate system
|
|
The
polar coordinate system is a two-dimensional coordinate system
in which each point P
on a plane is determined by the length of its position vector r
and the angle q
between it and the positive direction of the x-axis,
where 0 <
r
< + oo
and 0
<
q
< 2p.
|
|
|
Polar
and Cartesian coordinates relations
|
 |
| Since the inverse tangent function
(arctan or tan-1)
returns values in the range -p/2
< q <
p/2, then |
|
for points lying in the 2nd or 3rd quadrant |
and for points lying in the 4th quadrant |
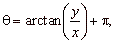 |
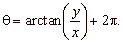 |
|
|
|
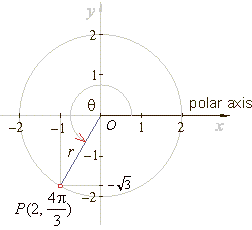
Example:
Convert Cartesian coordinates (-1,
-Ö3)
to polar coordinates.
|
|
Solution: |
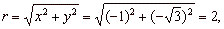 |
|
and since the point lies in the 3rd quadrant,
then |
|
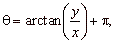 |
|
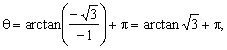 |
|
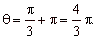 |
|
 |
|
|
|
::
Equation
of a line in polar form
|
|
Lines
parallel to the axes, horizontal and vertical lines
|
| Lines
parallel to the y-axis |
| A
vertical line, x
=
c is
represented by the equation |
| r
cosq
=
c
or |
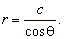 |
|
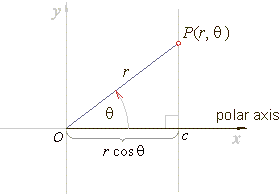 |
|
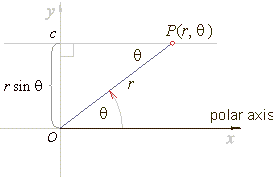
| Lines
parallel to the x-axis |
| A
horizontal line, y
=
c is
represented by the equation |
| r
sinq
=
c
or |
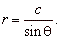 |
|
 |
|
|
Lines
running through the origin or pole (radial lines)
|
| The
equation of a line through the origin or pole that makes an angle
a with the positive
x-axis |
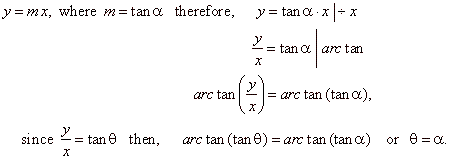 |
| Thus,
the
equation of a line through the origin is
represented by the equation q
=
a
in polar
coordinates. |
|
|
Polar
equation
of a line
|
|
|
|
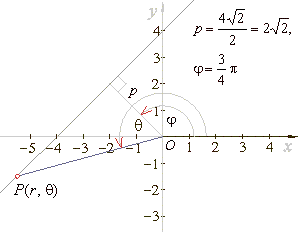
Example:
Write polar equation of the
line passing through points (-4,
0)
and (0, 4).
|
|
Solution: Using polar equation of a line |
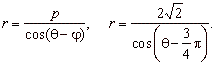 |
| Proof,
using Cartesian to polar
conversion formulas. |
| The
intercept form of the line |
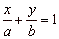 |
or |
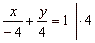 |
|
-
x
+ y =
4,
y
=
x
+ 4 |
|
 |
|
|
|
|
|
::
Equation
of a circle in polar form
|
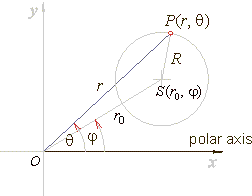
| General
equation of a circle in polar coordinates |
|
The
general equation of a circle with a center at |
|
(r0,
j)
and radius R. |
| Using
the law of cosine, |
| r2
+ r02
-
2rr0
cos(q
-
j)
=
R2 |
|
 |
|
|
Polar
equation of a circle with a center on the polar axis running
through the pole
|
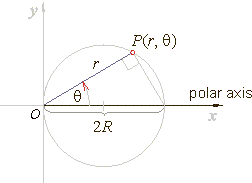
| Polar
equation of a circle with radius R
and a center on the polar axis running through the pole O
(origin). |
| Since |
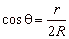 |
then, |
| r
=
2R
cosq |
|
 |
|
|
Polar
equation of a circle with a center at the pole
|
| Since,
r2
=
x2
+ y2
and x2
+ y2
=
R2
then r
=
R |
| is
polar
equation of a circle with radius R
and a center at the pole (origin). |
|
|
|
Example:
Convert the polar
equation of a circle r
=
-
4
cosq
into Cartesian coordinates.
|
|
Solution:
As, r
=
-
4
cosq
then r2
=
-
4r
cosq, |
| and
by using polar to Cartesian conversion formulas, r2
=
x2
+ y2
and x
=
r cosq |
| obtained
is
x2
+ y2
=
-
4x |
|
x2
+ 4x
+ y2
= 0
|
|
or
(x
+ 2)2 + y2
= 4
|
| the
equation of a circle with radius R
= 2 and
the
|
| center
at (-2,
0).
|
|
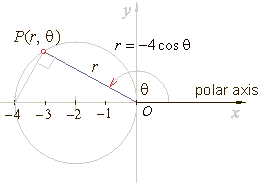 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
B
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|