|
|
|
|
ALGEBRA
|
|
|
|
Interest
calculation
|
|
::
Simple interest
|
|
An amount of money deposited into a bank for a given period of
time brings to the depositor a profit called interest.
|
|
Amount of interest,
principal (initial amount), interest rate and amount after n
years
|
|
The
amount of
interest ( I
) the bank pays you, depends on the
interest rate (
i % ),
the amount of money deposited, denoted as principal P
also called original balance (or
initial investment), and the period of
time n
the money is deposited,
|
|
since P
: I = 1 : (i · n)
then, |
 |
|
|
|
|
|
Simple interest is calculated on
a yearly basis (annually, n
= 1) in which balance grows linearly with
time (as opposed to compound interest).
|
|
If P
is the principal (or initial value of investment) and I
is the interest amount, the accumulated value A
(or final value of
investment) at the end of n
investment periods is given by
|
| A
= P + I = P + i · P · n = P (1 + i n) |
|
|
|
|
|
Example:
Somebody deposits $20,000 into a savings account
where the rate of interest is 4.8% annually.
How much money in interest will earn after nine months?
|
|
Solution:
|
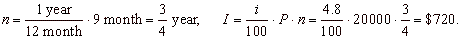 |
|
|
Example:
A bank lends a company money for the six months period at
a rate of 8% annually.
How much was lent if the company should pay $12,000 of interest?
|
|
Solution:
|
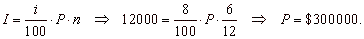 |
|
|
Example:
At what an interest rate was borrowed
$75,000 for one year if $3,000 to interest is charged?
|
|
Solution:
|
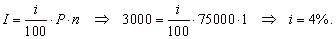 |
|
|
Example:
For what period of time should be deposited
$200,000 at a 6% interest rate to earn $6,000 of interest?
|
|
Solution:
|
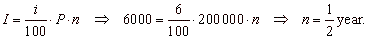 |
|
|
|
::
Compound interest
|
|
In compound interest calculations,
the interest earned in each period is added at the end of a
period to the principal of the previous period, to become the
principal for the next period.
|
|
The compounding periods can be yearly, semiannually, quarterly,
or the interest can be compounded more frequently even continuously.
|
|
Thus,
if P
is the principal or initial value of investment and the compound interest
rate is i %,
then
|
|
I1 = i P
is the amount of interest earned in the first period.
|
|
So,
at the end of the first period, the accumulated amount is
|
|
A1 = P + I1 = P
+ i P = P(1 + i).
|
|
Thus,
at the end of n
periods (or after n
years) the accumulated amount or final value of investment is
|
|
An
= A = P(1 + i)(1 + i) · · · (1 + i)
= P(1 + i)n
|
| or, |
An
= A = P · r
n,
where r
= 1 + i |
|
|
|
|
|
| Example:
After how many years will
deposit double at an interest rate of 6%. |
|
Solution:
|
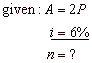 |
|
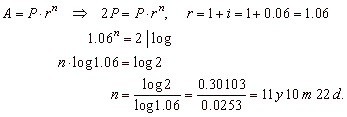 |
|
| Example:
At what annual interest
has to be deposited $5,000 for four years to grow to $8,000. |
|
Solution:
|
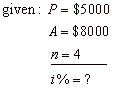 |
|
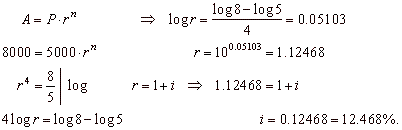 |
|
|
|
Periodic compounding
|
|
Note
that for any given interest rate the investment grows more if
the compounding period is shorter.
|
|
So,
if P is
an amount of money invested for n years at an interest rate
i, compounded
m times per year, then the total number of
compounded periods is m·n and the interest rate per period is
i/m
and the accumulated or future value is
|
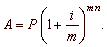
|
|
|
Example:
The principal amount of
$2,000 is invested for five years in a compound interest account
paying 6% compounded quarterly, find the final or accumulated
amount in the account.
|
|
Solution:
|
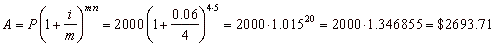 |
|
|
|
Continuous compounding
|
|
The formula for continuous compounding,
|
A
= P·ei·n
.
|
|
|
|
Example:
Suppose $5,000 is deposited into an account that pays interest
compounded continuously at an annual rate of 8%. How
much will the account be worth in 20 years?
|
|
Solution:
|
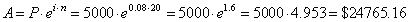 |
|
|
|
::
Exponential
growth and decay, application of the natural exponential
function
|
|
We
use the same formula as for continuous compound interest in many natural processes
where the rate of change of a
quantity through time is proportional to the current amount of the
quantity.
|
|
A
quantity is said to be subject to exponential growth if it
increases at a rate proportional to its current value.
|
|
The
constant k
is called the growth rate and in
exponential growth k
> 0. The rate constant k
depends only on the process and the conditions under which it is
carried out.
|
|
A
quantity is said to be subject to exponential decay if it
decreases at a rate proportional to its current value.
|
|
The
constant k
is called the decay
rate and in exponential decay k
< 0.
|
|
|
|
|
Example:
Suppose that
microorganisms in a culture dish grow exponentially. At the
start of an experiment there are 8,000 of bacteria, and two
hours later the population has increased to 8,600. How long will
it take for the population to reach 20,000?
|
|
Solution:
Given the initial
population N0
= 8,000 and for t
=
2 hours
the population increased to
N
= 8,600.
We
first find the growth rate k
and then the time needed the population increases to 20,000.
|
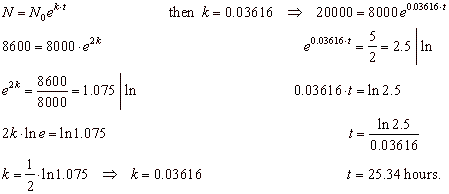 |
|
|
| Radioactive decay is a
typical example to which the exponential decay model can be
applied. |
| Example:
After 800
years a sample of radioisotope radium-226 has decayed to 70.71%
of its initial mass, find the half-life of radium-226. |
| Solution:
The half-life of a radioactive material is the amount of time
required for half of a given sample to decay. First
we plug the given information into the formula for exponential
decay |
| N(t)
= N0 ekt to
find the decay constant k. |
| Since
N0
is the initial quantity, N(t)
is the quantity after time t
and k
is the decay constant then, by
substituting
N(t = 800) = 0.7071·N0
into
the formula |
| 0.7071N0
= N0 e k · 800 |
|
and
solving for k,
0.7071 =
e k · 800
| ln |
|
ln 0.7071 = 800 · k |
|
k = ln (0.7071) / 800,
k = -
0.0004332217. |
| Thus,
the formula for the amount of radium-226 present at a time t
is |
| N(t)
= N0 e -
0.0004332217 · t
. |
| As
we want determine the half-life or the time for half of a substance to decay,
we substitute |
| N(t)
= (1/2) N0 into
the formula |
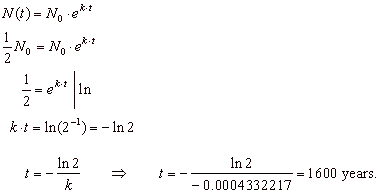 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
B
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|