|
::
Rules and properties of logarithms
|
| A
logarithm is the exponent (the power) to which a base must be
raised to yield a given number, that is |
| y =
loga
x
if x = a
y. |
|
|
| Examples: |
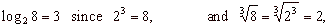 |
|
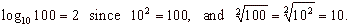 |
|
|
|
|
|
Logarithms
are used to simplify multiplication, division and exponentiation
so that,
|
|
loga
(m · n) =
loga
m +
loga
n
|
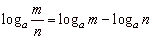
|
|
loga
mn =
n ·
loga
m
|
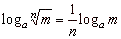
|
|
| Example: |
Using the rules of logarithms find the value of x. |
|
Solution: |
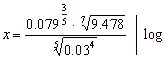 |
|
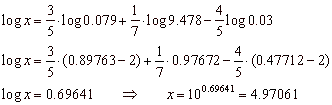 |
|
|
|
Changing the base – different
logarithmic identities
|
|
Using
the identity
|
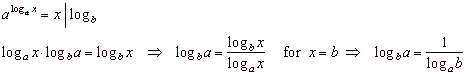
|
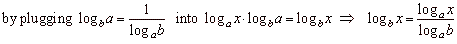
|
|
In
a similar way
|
|
|
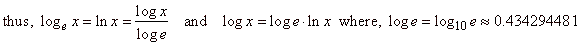
|
|
|
| therefore, |
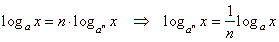 |
|
| Similarly, |
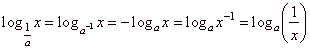 |
|
|
|
|
| Example: |
If log 2
x
= 7 then log
4 2x = ?. |
|
|
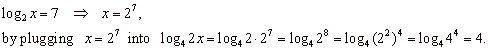 |
|
| Example: |
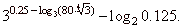 |
|
Solution: |
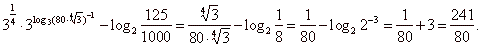 |
|
|
|
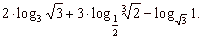 |
|
Solution: |
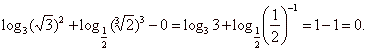 |
|
|
|
::
Exponential and logarithmic equations
|
|
Exponential equations
|
|
In
exponential equations the variable that has to be solved for is in
the exponent.
|
|
To
solve an exponential equation, rewrite the given equation to get
all powers (exponentials) with the same base, or use
logarithms when solving the exponential equation.
|
|
| Examples:
a) Solve 0.25x
= 43x
- 2 |
b) Solve 43x
+ 2
= 64 · 22x
- 4 |
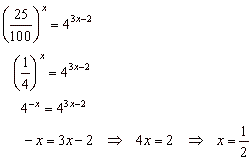 |
|
42
· 43x
= 43 · 22(x
- 2)
| ¸
42 |
|
43x
= 41 + x
- 2 |
|
3x = x
- 1 |
|
2x
= - 1
=>
x
= - 1/2. |
|
|
|
| Example:
Solve 4x
+ 2
+ 4x
+ 1
+ 4x
-1
= 3x
+ 3
+ 3x
+ 2.
|
|
|
|
|
| Example:
Solve
4x
-
2 =
5x.
|
|
|
|
|
Logarithmic equations
|
|
As
logarithmic equations contain a logarithm of variable quantity,
we use rules and properties of logarithms to solve a logarithm
equation.
|
|
| Example:
Solve log
x = -2. |
|
Solution: log
x = log10-2,
x = 10-2
= 0.01. |
|
| Example:
Solve log2
(log3 x) = 1. |
|
Solution:
log3 x
= 21,
x = 32
= 9. |
|
|
| Example:
Solve log
(x + 5) -
log
(2x -
3) = 2 · log 2.
|
|
|
|
|
| Example:
Solve log
(log
x) + log
(log
x3 -
2) = 0.
|
|
|
|
|