|
|
|
|
ALGEBRA
|
|
|
| Exponentiation
- powers or indices, rules and properties
|
| Exponentiation
properties |
Examples |
| 1 |
a
· a
· · · · a
= an,
n
factors |
1 |
a3
= a · a
· a,
24 =
2 · 2 ·
2 ·
2
= 16 |
| 2 |
a
= a1,
or a1
=
a |
2 |
2
= 21,
(-3)1
= -3 |
| 3 |
a0
= 1,
an ¸
an
= 1 |
3 |
23
¸ 23
= 23 -
3 =
20
= 1,
(ab3)0
= 1 |
| 4 |
1n
=
1 |
4 |
15
= 1, (-1)5
= -1 |
| 5 |
(-
a)2n
= a2n,
2n
-even exponent |
5 |
(-
5)4 = 54
= 625 |
| 6 |
(-
a)2n
-1
= - a2n
-1,
2n-1
-odd exponent |
6 |
(-
2)3 = -
23
=
- 8 |
| 7 |
(-1)2n
= 1 |
7 |
(-1)6
= 1 |
| 8 |
(-1)2n
-1
= -1 |
8 |
(-1)7
= -1 |
|
|
The
rules for powers (or exponents) |
| Rules |
Examples |
| 1 |
am
· an
= am
+
n, |
a)
a3
· a4 =
a3
+ 4,
b) 24
· 25 = 24 + 5 =
29 = 512, |
| 2 |
am
¸
an =
am
- n, |
a) x5
¸
x3
= x5
-
3
= x2,
b) 0.14
¸
0.13 = 0.14
-
3 = 0.1, |
| 3 |
an
· bn
= (a
· b)n, |
a) 24
· 34 = (2
· 3)4
= 64,
b) 45
· 0.85 = (4
· 0.8)5
= 3.25, |
| 4 |
an
¸
bn
= (a ¸
b)n, |
a) x6
¸
y6
=
(x
¸
y)6,
b) 125 ¸
35 = (12
¸
3)5 =
45, |
| 5 |
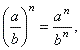 |
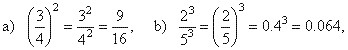 |
| 6 |
(am)n =
am
· n, |
a) (a3)4
= a3
·
4 = a12, b)
(45)3
= 45
·
3 = 415, |
| 7 |
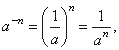 |
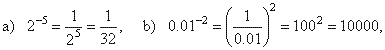 |
| 8 |
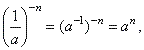 |
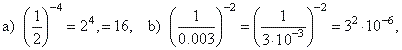 |
| 9 |
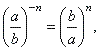 |
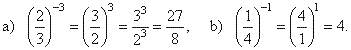 |
|
|
Radicals - Exponentiation with a fractional exponent
|
| Properties |
Examples |
|
If
m,
n and p
are natural numbers
(n
>1) and
if a
and b
are nonnegative
real numbers, then |
| 1 |
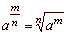 |
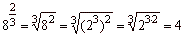 |
| 2 |
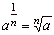 |
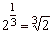 |
| 3 |
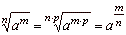 |
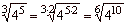 |
| 4 |
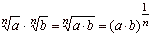 |
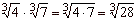 |
| 5 |
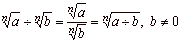 |
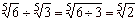 |
| 6 |
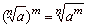 |
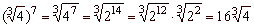 |
| 7 |
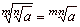 |
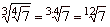 |
| 8 |
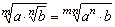 |
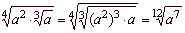 |
|
|
Rationalizing
denominator
|
| 1 |
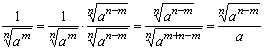 |
| Example |
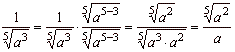 |
| 2 |
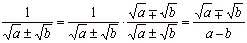 |
| Example |
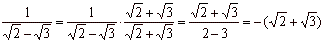 |
| 3 |
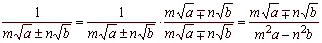 |
| Example |
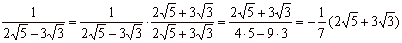 |
|
|
Algebraic
expressions - monomial, binomial, trinomial, . . . ,
polynomial
|
|
Expanding
algebraic expression by removing parentheses or brackets
|
|
The
square of binomial - perfect square trinomial |
Example |
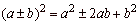 |
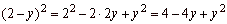 |
|
|
The
cube of binomial
|
Example |
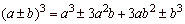 |
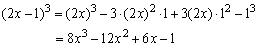 |
|
| The
binomial expansion algorithm
|
|
|
|
Factoring algebraic
expressions
|
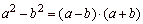 |
-
difference of two squares
|
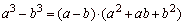 |
-
difference of two cubes |
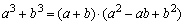 |
-
sum of two cubes |
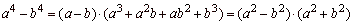 |
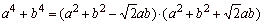 |
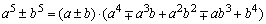 |
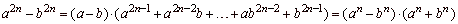 |
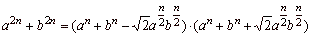 |
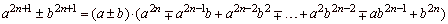 |
|
|
|
Ratios and
proportions
|
|
If a
: b = k
and c
: d = k, |
| then
a :
b = c : d
and a
×
d = b
×
c,
and
(a + b) : b = (c
+ d) : d, |
| (a
+ b) : a = (c + d)
: c,
(a -
b) : a = (c -
d) : c
and (a
+ b) : (a -
b) = (c + d) : (c
-
d). |
|
If a
: b = b :
c then |
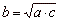 |
is
the
geometric mean |
|
If a1
: b1 = k,
a2
: b2 = k,
a3
: b3 = k, .
. . , an
: bn = k |
| then,
a1
: a2
: a3
: . . . : an
= b1
: b2 : b3
: . . . : bn
. |
|
| If given are
proportions: a
: b = i :
j, b :
c = k :
l and
c
:
d = m :
n |
|
then, a
: b = i :
j = (
i ×
k
×
m)
: (
j ×
k
×
m), |
|
b :
c = k : l = (
j ×
k
×
m)
: (
m ×
j
×
l) |
|
and c
: d = m : n = (m
×
j
×
l)
: (
n ×
j
×
l), |
|
follows a
: b : c : d = (
i ×
k
×
m)
: (
j ×
k
×
m)
: (
m ×
j
×
l)
: (
n ×
j
×
l). |
|
|
Example
|
| Given,
a
: b = 1 :
2 and
b :
c = 3
:
4 |
|
then, a
: b = 1 :
2 = (1
×
3)
: (2
×
3), |
|
b
:
c = 3
:
4 = (3
×
2)
: (4
×
2),
therefore a
: b :
c = 3 : 6 :
8. |
|
|
|
Percentage
|
| Denoting,
the base or whole value (x),
rate (p),
part of amount (y)
then, |
|
part
: whole =
rate
: 100
or y
: x =
p :
100
that is |
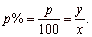 |
|
|
Examples
|
| a)
What is 5% of 30? From the proportion, |
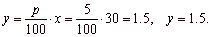 |
| b)
What is the base value if 15% of it is 30? |
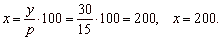 |
| c)
What percent of 30 is 27? |
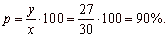 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents A
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|