ALGEBRA - solved problems
  Imaginary and complex numbers
     Imaginary numbers
114.    Reduce,  i15,  i26  and  i149.
Solutions:       i15 = i4 · 3 · i3 = i3 = - i,     i26 = i4 · 6 · i2 = i2 =  -1   and   i149 = i4 · 37 · i  =  i.
  Complex numbers
Addition and subtraction of complex numbers
115.
   Given are complex numbers,  z1 = -3 + 2i  and  z2 = 4 + 3i,  find  z1 + z2  and  z1 - z2.
Solutions:       z1 + z2 = (-3 + 2i) + (4 + 3i) = (-3 + 4) + (2 + 3)i = 1 + 5i
     and             z1 - z2 = (4 + 3i) - (1 + 5i) = (4 - 1) + (3 - 5)i = 3 - 2i
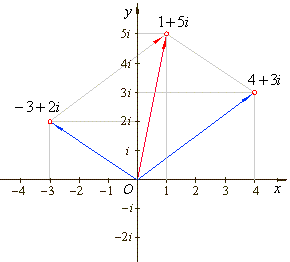
Given addition and subtraction are shown in the complex plane in the figures below.
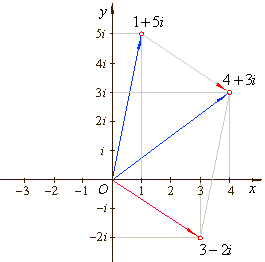
z1 + z2 = (-3 + 2i) + (4 + 3i) = 1 + 5i   z1 - z2 = (4 + 3i) - (1 + 5i) = 3 - 2i
   
Multiplication and division of complex numbers
116.
   Given are complex numbers,  z1 = -3 + 2i  and  z2 = 4 + 3i, find  z1 ·  z2  and  z1 / z2.
Solutions:       z1 ·  z2 = (-3 + 2i) · (4 + 3i) = -3 · 4 + 2 · 4i + (-3) · 3i +  2 · 3 i2 = -18 - i
and  
117.
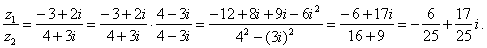   For what real number a the real part of the complex number 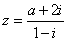equals 1.
Solution:
118.
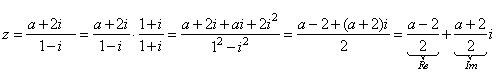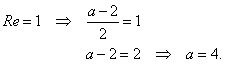   Evaluate the expression 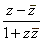where  z = 1 - i.
Solution:
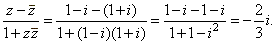Polar or trigonometric notation of complex numbers
119.    Given the complex number  z = 1 - Ö3 i,  express  z = x + yi  in the trigonometric form.
Solution:   The modulus
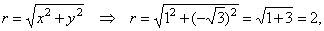                  the argument
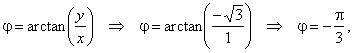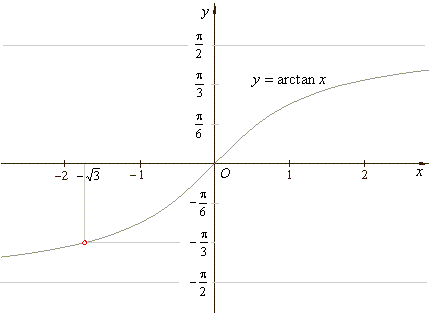
    the trigonometric form is
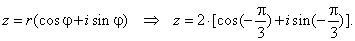Multiplication and division of complex numbers in the polar form
 If given    z1 = r1(cosj1 + isinj1)    and    z2 = r2(cosj2 + isinj2)
  then, z1 ·  z2 = r1 r2 · [cos(j1 + j2) + isin(j1 + j2)]
and
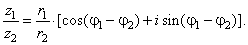Exponentiation and root extraction of complex numbers in the polar form - de Moivre's formula
We use the polar form for exponentiation and root extraction of complex numbers that are known as 
  de Moivre's formulas, zn = rn · [cos (nj) + isin (nj)]
and
120.
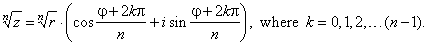   Calculate
Solution:
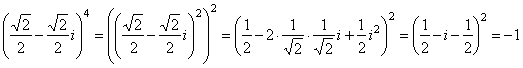or in the polar form,
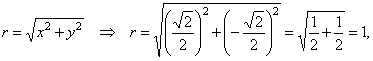and
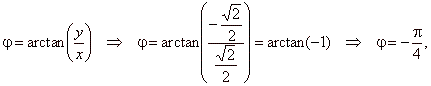since exponentiation with an integer exponent   zn = rn e inj = rn (cos nj + sin nj),
then
121.
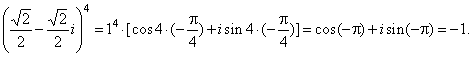   Compute
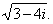Solution:   Since the square root of a complex number is a complex number, then
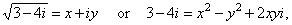
and, two complex numbers are equal if their real parts are equal and their imaginary parts are equal, that is
Solved problems contents
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.