|
|
|
ALGEBRA
- solved problems
|
|
|
|
|
|
|
|
|
| Interest
calculations |
| Compound interest |
|
| 38. |
If $10,000 is invested for
five years at 6% of the interest rate, find the accumulated or
final value and
|
|
| total interest earned at the end of the period
under both, simple and compound interest. |
| In compound interest calculations,
the interest earned in each period is added at the end of a
period to the principal of the previous period, to become the
principal for the next period. |
| The compounding periods can be yearly, semiannually, quarterly,
or the interest can be compounded more frequently even continuously. |
| If
P
is the principal or initial value of investment, A
is the accumulated amount or final value of investment and the compound interest
rate is i % |
|
then,
A = P · r
n,
where r
= 1 + i,
and where |
|
|
|
Solution:
Given,
P
= $10,000, p%
= 6%
and
n =
5 years, A and
I
=?
|
| a)
Under simple interest,
the total interest earned in five years period is |
|
I = i% · P · n =>
I = 6/100
· 10000 · 5 = $3000, |
| the accumulated value after five years period is |
|
A
= P + I = P (1 + i n)
=> A
= 10000 · (1 + 6/100 · 5) = 10000
· 1.3 = $13000, |
| so
that I
= A -
P
= 13000
-
10000 = $3000. |
|
b) Under compound interest,
the accumulated value after five years period is |
|
A
= P(1 + i%)n => A
= 10000 · (1 + 0.06)5
= 10000 · 1.338225 = $13382.25 |
| therefore, the total interest earned in five years period is |
|
I
= A -
P
= 13382.25
-
10000 =
$3382.25. |
| So,
the interest compounding (or interest earned on interest) brings
the extra $382.25 in
comparison with the simple interest. |
|
| 39. |
After how many years will
deposit double at an interest rate of 6%.
|
|
|
Solution: |
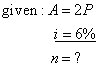 |
|
|
|
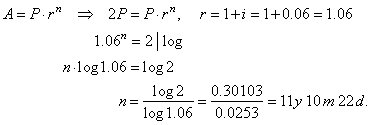 |
|
|
| 40. |
At what annual interest
has to be deposited $5,000 for four years to grow to $8,000.
|
|
|
Solution: |
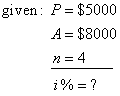 |
|
|
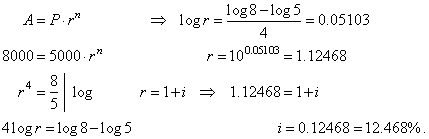 |
|
|
| Periodic compounding |
|
| 41. |
The principal amount of
$2,000 is invested for five years in a compound interest account
paying 6%
|
|
| compounded quarterly, find the final or accumulated
amount in the account. |
| Note
that for any given interest rate the investment grows more if
the compounding period is shorter. |
| So,
if P is
an amount of money invested for n years at an interest rate
i, compounded
m times per
year then, the total number of
compounded periods is mn and the interest rate per period is
i/m |
|
and the accumulated or future value is
|
 |
|
|
Solution: |
 |
|
|
| Continuous compounding |
|
| 42. |
Suppose $5,000 is deposited into an account that pays interest
compounded continuously at an
|
|
| annual rate of 8%. How
much will the account be worth in 20 years? |
| As for any given interest rate the investment grows more if the compounding period is shorter, we let the number of periods in a year
approach infinity to compound the interest continuously, meaning that the
balance grows by a small amount every instant. |
| Thus,
to derive a formula for continuous compounding we need to
evaluate the above formula when m
tends to infinity (i.e., the year is divided into infinite
number of periods) |
 |
| then
by substituting |
 |
and,
when m ®
oo
then x ®
oo, |
|
|
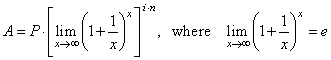 |
| that
is, the limit in the square brackets converges to the number e = 2.71828 . . . ,
thus obtained is |
| the
continuous compounding formula A
= P · e i n,
where e
is the base of natural logarithms. |
|
Solution: |
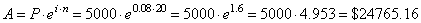 |
|
|
| Exponential
growth and decay, application of the natural exponential
function |
|
| 43. |
Suppose that
microorganisms in a culture dish grow exponentially. At the
start of an experiment
|
|
| there are 8,000 of bacteria, and two
hours later the population has increased to 8,600. |
| How long will
it take for the population to reach 20,000? |
|
Solution: Given the initial
population N0
= 8,000 and for t
=
2 hours
the population increased to N
= 8,600. |
| We
first find the growth rate k
and then the time needed the population increases to 20,000. |
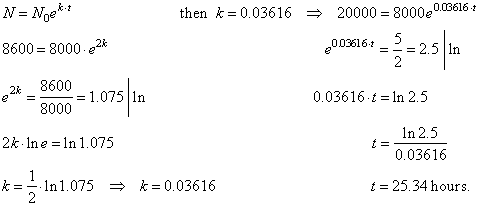 |
|
| 44. |
After 800
years a sample of radioisotope radium-226 has decayed to 70.71%
of its initial mass, find
|
|
| the half-life of radium-226. |
| Radioactive decay is a
typical example to which the exponential decay model can be
applied. |
|
Solution:
The half-life of a radioactive material is the amount of time
required for half of a given sample to |
| decay.
First
we plug the given information into the formula for exponential
decay |
|
N(t)
= N0 ekt to
find the decay constant k. |
| Since
N0
is the initial quantity, N(t)
is the quantity after time t
and k
is the decay constant then, |
| by
substituting
N(t = 800) = 0.7071·N0 into
the formula |
| 0.7071N0
= N0 e k · 800 |
| and
solving for k,
0.7071 =
e k · 800
| ln |
|
ln 0.7071 = 800 · k |
|
k = ln (0.7071) / 800 |
|
k = -
0.0004332217. |
| Thus,
the formula for the amount of radium-226 present at a time t
is |
| N(t)
= N0 e -
0.0004332217 · t |
| As
we want determine the half-life or the time for half of a substance to decay,
we substitute N(t)
= (1/2) N0 |
| into
the formula |
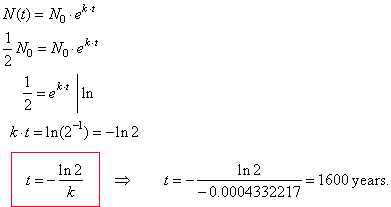 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |