|
|
|
ALGEBRA
- solved problems
|
|
|
|
|
|
|
|
|
|
Ratios and proportions
|
|
Ratios and proportion properties
|
|
|
| 22. |
Write a proportion by given ratios.
|
|
| Solution: |
|
9
: 6 = 3/2
and, 21
: 14 = 3/2,
follows,
9 :
6 = 21 : 14. |
|
|
A proportion is
a statement of the equality of two ratios. If the fractions both reduce
to the same value, the proportion is true.
|
|
|
| 23. |
Use ratios and proportion properties to rewrite
given expressions.
|
|
| Solutions: |
Since, |
a
:
b =
(a · c)
:
(b ·
c) |
then
|
a) |
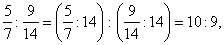 |
|
and |
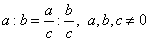 |
|
b) |
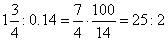 |
|
|
|
|
Direct and inverse proportion
|
|
| 24. |
A lift reaches the third floor in seven seconds. When will reach
the 18th floor?
|
|
| Solution: |
Given quantities make the proportion |
|
| |
x1
:
y1 =
x2
:
y2. |
That
is, |
3
:
7 =
18 :
x |
=> |
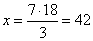 |
seconds. |
|
|
| We could obtain the same result by setting up the corresponding
values of the proportional quantities in a table where arrows show the sequence of the terms of the proportion. |
| |
ß |
3rd
floor |
|
ß |
7
sec. |
|
|
| |
18th
floor |
|
x
sec. |
or |
3
:
18 = 7 :
x |
|
| |
|
|
| => |
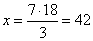 |
seconds. |
|
|
|
| 25. |
To
the central angle a = 30°, of a circle of radius
r, corresponds
the arc length equal
p/6
r.
|
|
|
What arc length corresponds to the
central angle a = 320°?
|
|
|
|
|
| 26. |
If 12 workers can do a job in 15 hours, then how many workers
would be needed to do the job in 9
|
|
|
hours?
|
| Solution: |
It’s obvious that more workers will do a job in shorter time. That
means, the time it takes to do |
|
|
the job is inversely proportional to the
number of workers.
|
| Therefore, use the proportion or set up the
table where the corresponding values make the colons and the arrows show the sequence of the terms of the proportion.
|
| |
ß |
12
workers |
|
Ý |
15
hours |
|
|
| Thus, |
x
workers |
|
9
hours |
or |
12
:
x =
9 :
15 |
|
| |
|
|
| => |
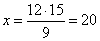 |
workers. |
|
|
|
| 27. |
A distance
d
from place A to place B a car covers in 75 minutes
traveling at the rate of 120 km/h.
|
|
| At what rate it should drive so that
it will travel the same distance in 60 minutes. |
| Solution: |
By driving two times
faster, the same distance it will cover in half less time. |
|
| Since, rate
r and time
t are inversely proportional quantities use the proportion
x1
:
x2 =
y2
:
y1. |
|
As the quantities we are comparing must always
be measured in the same units, we’ll convert minutes to hours,
so 75 min =
75
min
· 1hour
/ 60
min =
1.25
h.
|
| |
ß |
1.25
h |
|
Ý |
120
km/h |
|
|
| Thus, |
1
h |
|
x
km/h |
or |
1.25
:
1
= x :
120 |
|
| |
|
|
| => |
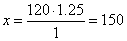 |
km/h. |
|
|
|
|
|
Percent
or percentage
|
|
Percent, decimal number and
fraction conversions
|
|
|
| 28. |
As appropriate, given
values convert
to, a percent, a decimal number and a fraction.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |