Limit of function, Continuous function, Limits at infinity, Limits of functions as x approaches positive or negative infinity, Vertical asymptote, Horizontal asymptote, Slant or oblique asymptote

ALGEBRA - solved problems

The limit of a function

The limit of a function is a real number L that f (x) approaches as x approaches a given real number a, written

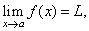if for any e > 0 there is a d (e) > 0 such that | f (x) - L | < e whenever | x - a | < d (e).

Continuous function

A real function y = f (x) is continuous at a point a if it is defined at x = a and

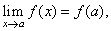that is, if for every e > 0 there is a d (e) > 0 such that | f (x) - f (a) | < e whenever | x - a | < d(e).

Limits at infinity (or limits of functions as x approaches positive or negative infinity)

401.

Evaluate the following limits,

Solution: a) As x tends to minus infinity f (x) gets closer and closer to 0. As x tends to plus infinity f (x) gets closer and closer to 0. Therefore,

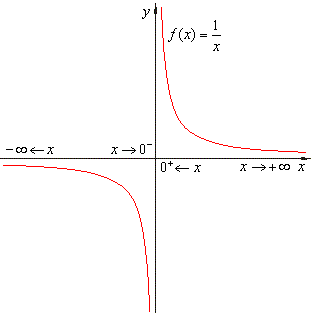
b) As x tends to 0 from the left f (x) gets larger in negative sense. As x tends to 0 from the right f (x) gets larger in positive sense. Thus,

Vertical asymptote

If there exists a number a such that

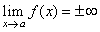then the line x = a is the vertical asymptote.

Horizontal asymptote

If there exists a number c such that

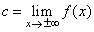then the line y = c is the horizontal asymptote.

Slant or oblique asymptote

If there exist limits

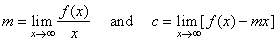then, a line y = mx + c is the slant asymptote of the function f (x).

402.

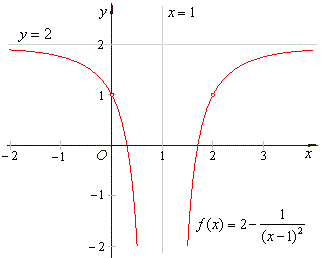
Find the vertical and the horizontal asymptote of the function

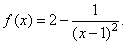Solution: Since,

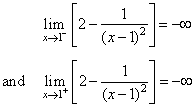then x = 1 is the vertical asymptote.

And since,

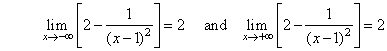then y = 2 is the horizontal asymptote.

403.

Calculate asymptotes and sketch the graph of the function

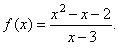Solution: By equating the numerator with zero and solving for x we find the x-intercepts,

x² - x - 2 = (x + 1)(x - 2) = 0,

x₁ = -1 and x₂ = 2.

We calculate f (0) to find the y-intercept,

f (0) = 2/3.

By equating the denominator with zero and solving for x we find the vertical asymptote,

x = 3.

Let calculate following limits

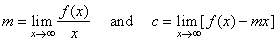to find the slant asymptote y = mx + c.

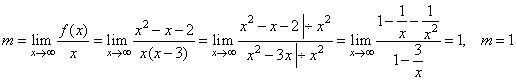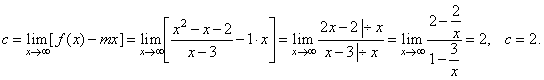Therefore, the line y = x + 2 is the slant asymptote of the given function.

404.

Find the following limits,

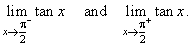Solution: The graph of the tangent function shows,

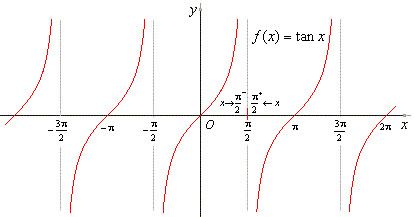as x approaches p/2 from the left, the tangent function increases to plus infinity, while as x approaches p/2 from the right, the function decreases to minus infinity, therefore

405.

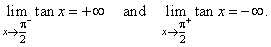Evaluate the limit

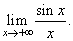Solution:

406.

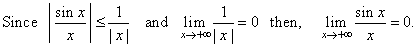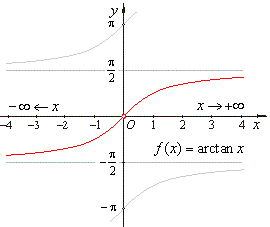
Evaluate the limit

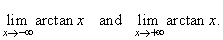Solution: The graph of the arc-tangent function shows, as x tends to minus infinity the function values approach - p/2 while, as x tends to plus infinity, the function values approach p/2.

Therefore,

and

Solved problems contents - A