|
|
Vectors in a Plane and Space |
|
|
|
|
|
Vectors
in a Plane |
Vectors - introduction |
|
Length, magnitude or
norm of the vector |
|
Collinear, opposite
and coplanar vectors |
|
Addition of vectors |
|
Triangle rule (law)
and parallelogram rule |
|
Zero or null vector |
|
Subtraction of vectors |
|
Scalar multiplication
or multiplication of a vector by scalar |
|
Unit vector |
|
Addition, subtraction
and scalar multiplication of vectors, examples |
|
Linear combination of
vectors |
|
Linear dependence of
vectors |
|
|
|
|
|
|
| Vectors - introduction |
There are physical quantities like force, velocity, acceleration and others that are not fully determined by their
numerical data.
|
| For example, a numerical value of speed of motion, or electric or magnetic field strength, not
give us the information about direction it move or direction they act.
|
Such quantities, which are completely specified by a magnitude and a direction, are called vectors or vector
quantities and are represented by directed line segment. |
| Thus,
a vector is denoted as
|
 |
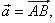where the point
|
|
|
A is called the tail or start and point
B, the head or
tip.
|
| The length or magnitude or norm of the vector
a
or |
 |
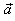is |
|
|
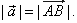
| Therefore, the length of the arrow represents the vector's magnitude, while
the direction in which the arrow points, represents the vector's direction. |
|
 |
|
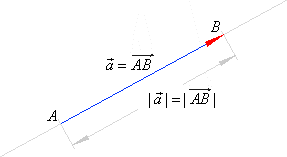| A vector with no magnitude, i.e., if the tail and the head coincide, is called the
zero or null vector
denoted |
 |
|
|
| Collinear, opposite
and coplanar vectors |
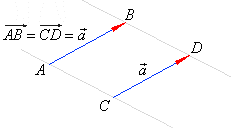
| Two vectors are said to be
equal if they have the same magnitude
and direction or if by parallel shift or translation one could be
brought into coincidence with the other, tail to tail and head to
head.
|
|
 |
|
| Vectors are said to be
collinear if they lye on the same line or on
parallel lines.
|
|
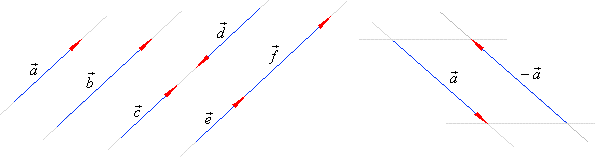
| Vectors,
|
 |
in
the above figure are
collinear. |
|
| Two collinear vectors of the same magnitudes but opposite directions are said to be
opposite vectors. |
| A vector that is opposite to |
|
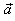is
denoted |
 |
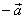as shows the
above right figure. |
|
Three or more vectors are said to be
coplanar if they lie on the same plane. If two of three vectors are
collinear then these vectors are coplanar.
|
| To prove this statement, take vectors,
|
 |
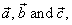of which
|
 |
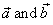are
collinear.
|
|
|
By using translation bring the tails of all three vectors at the same point. Then, the common line of
vectors,
|
|
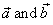and the line in which lies the vector
|
 |
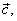determine the unique plane. |
|
| Therefore, if vectors are
parallel to a given plane, then they are coplanar.
|
|
| Addition of vectors |
| The sum of vectors, |
|
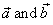can be obtained graphically by placing the tail of |
 |
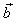to the tip or head of |
|
|
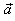| using translation.
Then, draw an arrow from the initial point (tail) of |
|
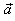to the endpoint
(tip) of |
|
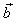to obtain |
|
| the
result. |
 |
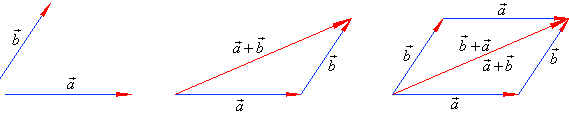| The
parallelogram in the above figure shows the addition |
 |
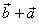where, to the tip of |
 |
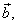by translation, placed |
|
| is the tail of |
|
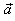then, drawn
is the resultant |
|
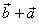by joining the tail of |
|
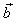to the tip of |
 |
|
|
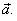| Note that the tips of the resultant and the second summand should coincide. |
| Thus, in the above figure
shown is, the triangle
rule (law) and the parallelogram
rule for finding the
resultant or
the addition of the two given vectors. The result is the same
vector, that is |
 |
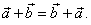| Therefore, vector addition is commutative. |
| Since vectors, |
 |
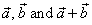form a triangle, they lie on the same
plane, meaning they are coplanar. |
|
| |
| Addition of three vectors,
|
 |
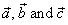is defined as
|
 |
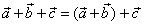and represented graphically
|
|
|
|
| The
above diagrams show that vector addition is
associative, that is |
 |
|
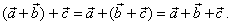| The same way defined is the sum of four vectors. |
|
 |
|
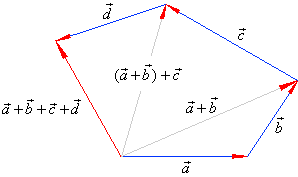| If by adding vectors obtained is a closed polygon,
then the sum is a null vector. |
 |
|
|
|
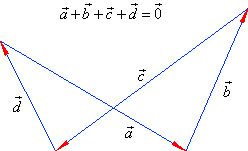| By adding a vector |
|
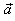to its opposite vector |
|
,
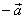graphically it leads back to the initial point, therefore |
|
|
 |
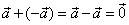so, the
result is the null vector. |
|
|
| Subtraction of vectors |
| Subtraction of two vectors,
|
|
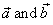is defined as addition of vectors
|
 |
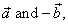that is,
|
|
|
 |
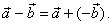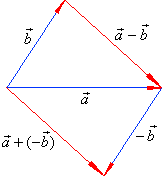
| As shows
the right figure, subtraction of two vectors can be accomplished directly.
|
| By using translation place tails of both vectors at the same
point and connect their
tips. |
| Note
that the arrow (tip) of the difference
coincides with the tip of the first
vector ( minuend). |
|
 |
|
|
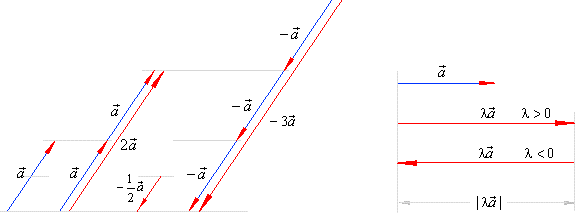
| Scalar multiplication
or multiplication of a vector by scalar
|
| Scalar is a quantity which is fully expressed by its magnitude or size
like length, time, mass, etc. as any real number.
|
| By multiplying a vector
a
by a real number
l
obtained is the vector l
a
collinear to
a
but,
|
| l times longer
then a
if | l
| > 1,
or shorter then a
if | l
| < 1,
and |
|
directed as a
if l
> 0,
or opposite to a
if l
< 0,
|
|
as is shown in the below figure.
|
 |
|
| Thus, the magnitude of the vector
l
a
equals to the product of the absolute value of the real number
l
and the magnitude of the vector a, that is |
 |
|
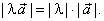| Besides, for the multiplication of a vector by a real number
following rules hold:
|
| 1)
l
· ( a + b ) = l
a + l
b |
| 2)
( l
+ m
) · a = l
a + m
a,
l,
m
Î R |
| 3)
l
( m
a ) = m
( l
a ) = ( m
l
) a |
| 4)
1 · a = a,
-1
· a = -
a |
| 5)
0 · a = 0,
m
· 0 = 0 |
|
 |
|
|
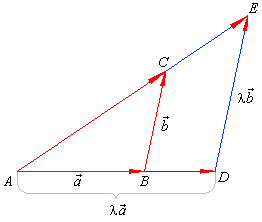
| In the similar triangles
ABC and
ADE
in the
right |
| figure,
AE
: AC
= DE
: BC
= AD
: AB
= l |
| therefore,
AE
= l
· AC. |
| Since
AE
= l
a + l
b
and AC
= a + b |
| then,
l
a + l
b = l
· ( a + b ). |
|
 |
|
|
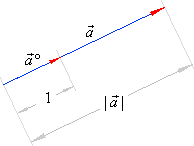
| Unit vector |
| A vector
|
 |
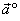is called the
unit vector of a vector
|
|
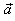if
|
 |
|
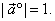| Therefore,
|
 |
|
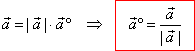| the unit vector
|
|
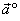determines the direction of the vector
|
|
|
|
 |
|
|
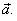| Addition, subtraction
and scalar multiplication of vectors, examples |
| Example: |
Given are vectors,
|
|
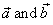determine
|
 |
|
|
|
|
|
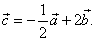| Example:
Given is a regular hexagon
ABCDEF with the center
O. Express vectors
CD,
BE,
EA,
and CE,
in terms of vectors, AB
= a
and BC
= b.
|
| Solution:
|
|
|
 |
 |
|
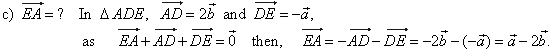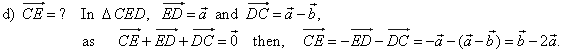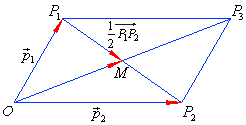
| Example: Determine the distance of the midpoint
M, of the segment
P1P2, and the point
O, if points,
P1
and P2
are heads of vectors p1
and p2 respectively, and whose tails coincide
with the point O
as shows the figure. |
| Solution: The
vector P1P2
represents the difference p2
-
p1. |
|
 |
|
 |
|
|
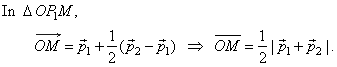| Example: In a triangle
ABC drown are medians as vectors,
|
 |
|
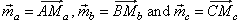| Prove
that
|
 |
|
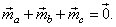| Solution:
Replacing the sides of the triangle by vectors, directed as in
the diagram,
|
 |
|
|
|
|
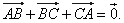| Example:
Use vectors to prove that line segments joining the midpoints of adjacent sides of a quadrangle,
form a parallelogram.
|
| Solution: The sides of the quadrangle ABCD are replaced by vectors, directed as in
the diagram so that the opposite vectors connecting midpoints are, |
|
|
| As equal vectors are of same lengths and parallel, therefore the line segments connecting the midpoints of any quadrangle, form a parallelogram. |
|
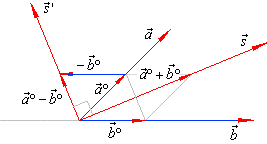
| Example:
Determine a vector which coincides with the angle bisectors of vectors, a
and b
in the diagram.
|
| Solution: The unit vectors of the given vectors
are, |
 |
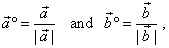| and they form a rhombus whose diagonal is |
 |
|
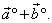| That is, a vector |
 |
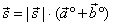will coincide
with |
|
| the angle bisector, while a vector |
 |
|
|
 |
|
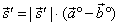| defines
the angle bisector of the supplementary angle of vectors, a
and b.
|
|
| Linear combination of
vectors |
| A vector
d
= l
a
+ m
b,
l, m
Î R
denotes the linear combination of the vectors, shown in the
left diagram. |
 |
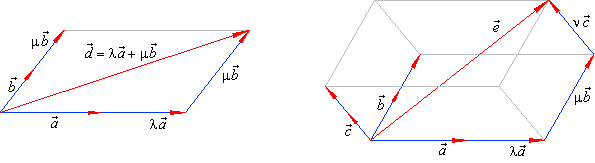| On the same way, the vector
e
= l
a
+ m
b
+ n
c
represents the linear combination of the vectors, a,
b
and c,
as shows the right diagram in the above figure. |
|
| Example:
Given is a parallelogram ABCD, the midpoint
M
of the side AD
and the intersection point O
of the diagonals. Express vectors,
AO,
BD,
and BM
as the linear combination of vectors,
a
= AB
and
b
= AD.
|
|
|
|
|
|
|
|
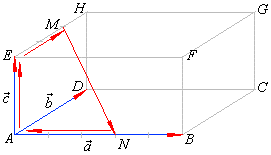
| Example:
To a cuboid ABCDEFGH
the point
M
divides the edge EH
in the ratio EM
: MH
= 2 : 1 and the
point N
the edge AB
in the ratio AN
: NB
= 3 : 2. Express the vector
MN
as the linear combination of vectors, a
= AB, b
= AD
and c
= AE.
|
|
|
 |
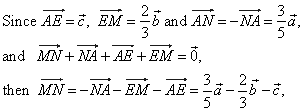| MN
is the linear
combination
of the vectors, a,
b
and c. |
|
|
 |
|
|
| Linear dependence of
vectors |
| Vectors,
a
= OA
and b
= OB
whose points,
O, A and
B
all lie on the same line are said to be linear
dependent, but if the points,
O, A and
B
do not all lie on the same line then a
and b, are not collinear, and are said to be
linear independent. |
|
a)
If a
and b
are linear independent vectors then every vector
d
of the plane determined by a
and b, can be
written as the linear combination of these vectors, that is in the form |
 |
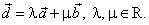| Vectors,
a
= OA, b
= OB and
c
= OC,
whose points,
O, A,
B
and C
all lie on the same plane, are said to be coplanar or linear dependent.
But if points, O, A,
B and
C
do not all lie on the same plane, then a,
b
and c
are not coplanar, and are said to be linear independent. |
b) If, a,
b
and c are linear independent vectors in 3D space then every vector
d, from the space, can be
represented as |
 |
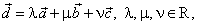| that is, as the linear combination of the vectors,
a,
b
and c. |
| Thus, in the
last example the sides of the cuboid are replaced by three linear independent vectors,
a,
b
and c
so that the vector MN
can be written as the linear combination of the vectors, a,
b
and c. |
|
|
|
|
