|
| Trigonometry |
|
|
|
|
 Trigonometric
functions of arcs from 0
to ±
2p
Trigonometric
functions of arcs from 0
to ±
2p
|
|
Trigonometric
functions of arcs that differ on p/2 |
|
Trigonometric
functions of arcs that differ on p |
|
Trigonometric
functions of arcs whose
sum is
2p |
|
Trigonometric
functions of angles lying on axes |
|
|
|
|
|
|
|
|
Trigonometric
functions of arcs that differ on p/2
|
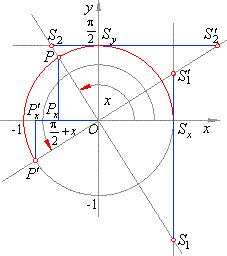
| Comparing the corresponding sides of the congruent right-angled
triangles,
in the right figure, we get the relations of trigonometric functions of
an arc x and
the arc p/2
+ x |
| |
Px′P′
= OPx => |
sin
(p/2
+ x) = cos x
|
|
|
| |
OPx′
= -PxP
=> |
cos
(p/2
+ x) = -sin
x
|
|
|
| |
SxS1′
= -SyS2 => |
tan
(p/2
+ x) = -cot x
|
|
|
| |
SyS2′
= -SxS1 =>
|
cot
(p/2
+ x) = -tan x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
corresponding function of angle which differ from the given for
90° (p/2).
|
|
a) sin
1,
b) cos 150°,
c) tan (-7p/4),
d) cot 50°.
|
| Solution:
a) sin
1 = -
cos (p/2
+ 1)
= -
cos 2.570796... |
|
b) cos 150°
= cos
(90°
+ 60°) = -
sin 60°
|
|
c) tan (-7p/4)
= -
cot (p/2
-
7p/4)
= -
cot ( -
5p/4)
= cot
(p
+ p/4) =
cot
p/4
|
|
d) cot 50°
= -
tan
(90°
+ 50°) = -
tan 140°.
|
|
|
|
Trigonometric
functions of arcs that differ on p
|
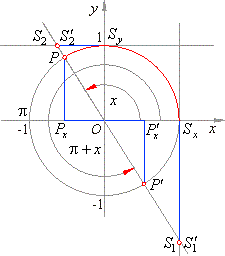
| Comparing the corresponding sides of the congruent right-angled |
| triangles,
in the right figure, we get the relations of trigonometric
|
| functions of
an arc x and
the arc p
+ x |
|
| |
Px′P′
= -PxP
=> |
sin
(p
+ x) = -sin
x
|
|
|
| |
OPx′
= -OPx
=> |
cos
(p
+ x) = -cos
x
|
|
|
| |
SxS1′
= SxS1 => |
tan
(p
+ x) = tan
x
|
|
|
| |
SyS2′
= SyS2 => |
cot
(p
+ x) = cot
x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
corresponding function of angle which differ from the given for
180° (p).
|
|
a) sin
235°,
b) cos p/6,
c) tan (-300°),
d) cot 4.
|
| Solution:
a) sin
235°
= sin (180°
+ 55°) = -
sin 55°
|
|
b) cos p/6
= -
cos (p
+ p/6) =
-
cos
7p/6
|
|
c) tan (-300°)
= tan (180° -
300°) = tan (-120°)
= -
tan 120°
|
|
d) cot 4
= cot (p
+ 0.858407...) = cot 0.858407....
|
|
|
| Example:
Simplify expression
cot (p
-
x)
· cos
(p/2
+ x)
+ tan (p/2
-
x)
· tan
(p
+ x) -
cos (-
x)
|
| Solution:
cot (p
-
x)
· cos
(p/2
+ x)
+ tan (p/2
-
x)
· tan
(p
+ x) -
cos (-
x) = |
|
= -
cot x
· ( -
sin x)
+ cot x
· tan x
-
cos x = cos x
+ 1 -
cos x =
1.
|
|
|
|
Trigonometric
functions of arcs whose
sum is 2p
|
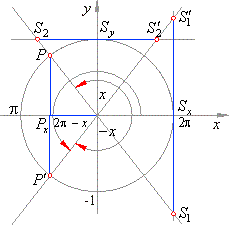
| The
right figure shows relations between sides of the congruent |
| right-angled triangles as
follows,
|
|
| |
PxP′
= -PxP
=> |
sin
(2p
-
x) = -sin
x
|
|
|
| OPx
= cos (2p
-
x)
= cos x |
cos
(2p
-
x) = cos
x
|
|
|
| |
SxS1′
= -SxS1
=> |
tan
(2p
-
x) = -tan
x
|
|
|
| |
SyS2′
= -SyS2
=> |
cot
(2p
-
x) = -cot
x
|
|
|
|
 |
|
|
|
| Example:
Trigonometric functions of a given arc, angle or number should be expressed by the
|
|
corresponding function of angle which when added with a given make
360° (2p).
|
|
a) sin
p/3,
b) cos 1,
c) tan 330°,
d) cot 10p/11.
|
| Solution:
a) sin
p/3
= -sin (2p
-
p/3) =
-
sin 5p/3 |
|
b) cos 1 = -
cos (2p
-
1) = cos 5.283185...
|
|
c) tan 330° =
tan (360° -
330°) = -
tan 30°
|
|
d) cot 10p/11
= -
cot (2p
-
10p/11) =
-
cot p/11.
|
|
|
| Example:
Prove that sin
320°
+ cos 50° = 0.
|
| Solution:
Since
sin 320° = sin (360°
-
40°) = -
sin 40°, and as
cos 50° = sin 40° |
|
then
-
sin 40°
+ sin
40° = 0.
|
|
|
| Example:
Calculate, sin
3p/2
· cos(-
p)
+ tan 5p/4.
|
| Solution: sin
3p/2
· cos(-
p)
+ tan 5p/4
= -
1 · (-
1) + tan (p
+ p/4)
= 1 + tan p/4
= 1 + 1 = 2. |
|
|
| Example:
Calculate, |
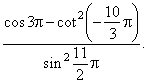 |
|
|
Solution:
|
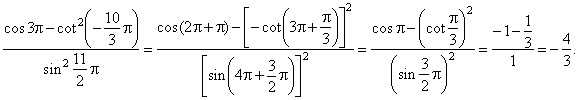
|
|
|
|
Example:
Prove the identity,
|
|
cos2 p/3
· sin (p/2
-
x) -
cos (p
-
x)
· cos2 p/6
= tan (p/2 +
x)
· sin (2p
-
x).
|
|
Solution:
Since sin
(p/2
-
x) = cos
x,
cos (p
-
x) = -
cos
x, tan (p/2 +
x) = -
cot
x
|
|
and sin
(2p
-
x) = -
sin x
then,
|
|
(cos p/3)2
· cos
x -
(-
cos
x)
· (cos p/6)2
= -
cot
x
· (-
sin x),
|
|
(1/2)2
· cos
x + (Ö3/2)2
· cos
x = (cos
x/sin x)
· sin x
=> cos
x = cos
x.
|
|
|
|
Example:
Prove the identity,
|
|
cot2 (p +
x)
· cos2 (p/2 +
x) + sin (-
x) · sin (p +
x) = tan (2p
-
x) · cot (-
x).
|
|
Solution:
[cot (p +
x)]2
· [cos (p/2 +
x)]2 +
(-
sin x)
· sin (p +
x) = (-
tan x)
· (-
cot x),
|
|
(cot
x)2
· (-
sin x)2
+ (-
sin x) · (-
sin x) = (sin x/cos
x)
· (cos
x/sin x)
|
|
cos2
x + sin2
x = (sin x/cos
x)
· (cos
x/sin x) = 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |