|
| Trigonometry |
|
|
Graphs of
Trigonometric Functions |
|
The
Graph of the Function y = asin
(bx + c) |
|
The function y = asin
x
|
|
The function y = sin
bx |
|
The function y = sin
(x + c)
|
 The function y = asin
(bx
+ c)
The function y = asin
(bx
+ c) |
|
|
|
|
|
|
|
| The
graph of the function y = a
sin
(b
x + c) |
|
The trigonometric functions of this form have wide application in physics, electricity and engineering where
are used in analyzing and modeling behavior of different situations in which things follow a repeating pattern. |
| Therefore, we need to know how the parameters
a,
b
and c
affect the form of the source sine function
y =
sin x. |
|
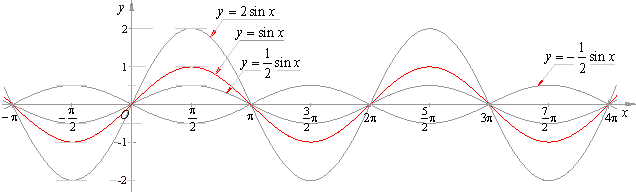
| The function y = a
sin
x |
| The graph of the function
asin x is obtained by multiplying each function value
sin x by the constant a. |
| That means, the ordinates of each point of the function
sin x should be a
times, |
| - increased if
a > 0 |
| - decreased if
0 < a < 1 |
| - while if
a < 1 each point of the graph should at the same time be flipped around
x-axis. |
| The parameter
a
is called amplitude. |
 |
|
|
The function y = sin
bx |
| The parameter
b
indicates the number of times function repeats itself within the period of
2p. Since there are
b
periods of the given function in
2p, then the length of its period is
P = 2p/b.
|
| The principal period
P
should satisfy identity for the periodic functions, thus |
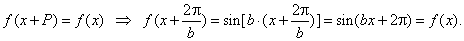 |
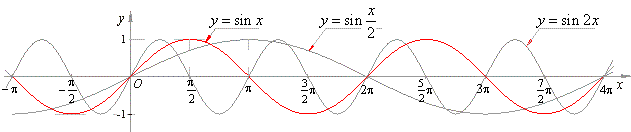
| For example, least or principal period of the function
sin 2x, |
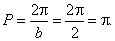 |
What means, its graph |
|
|
repeats twice within the period of
2p. |
| While the function |
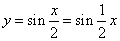 |
has a half of its period within the
interval of 2p, as its principal |
|
| period |
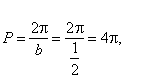 |
as can be seen in
the figure below. |
|
 |
|
|
The function y = sin
(x + c) |
|
The parameter c
represents the value of translation of the
sin x function in the direction of the
x-axis that is |
| f
(x) = sin x => f
(x -
x0) = sin
(x -
c), x0 =
c. |
| For example, the graph of the function
y = sin
(x -
p/6)
is obtained by translating the
sin x function horizontally to
the right by
x =
p/6,
as shows the graph below.
|
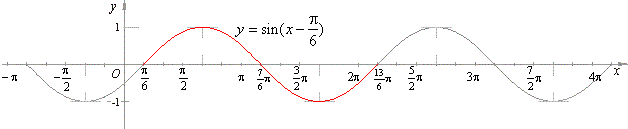 |
|
|
The function y = asin
(bx
+ c) |
| The graph of the
sin x function repeat once while its argument passes through all the values of an interval,
[x,
x + 2p] of the length
2p. |
| Therefore, the function
y = a
sin (bx + c) will repeat once while its argument
(bx + c)
passes through all the values
from 0
to 2p, that is |
| 0
<
bx + c <
2p |
| from
where bx
+ c > 0
=> x >
-
c/b
and bx
+ c <
2p
=> x <
-
c/b + 2p/b. |
| That means, the given function will start its period at
x = -
c/b
and end at the point x =
-
c/b + 2p/b. |
| It follows that the least or principal period of the function
y = a
sin (bx + c),
P = 2p/b.
|
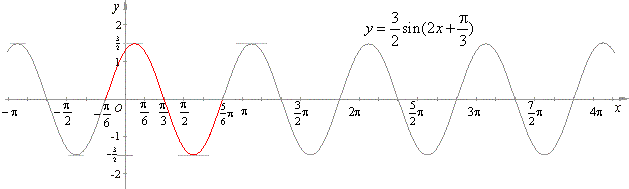
| For example the function |
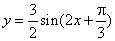 |
will repeat once in the interval |
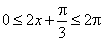 |
that is |
|
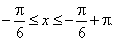 |
Thus, given function will repeat once in each interval of the length
p, or
P = p, while
|
|
| the initial point of the given interval is at
x = -
p/6,
as is shown in the figure below. |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |