|
| Sequences and
Series
|
|
| Sequences
|
Geometric sequence/progression |
|
General term of a geometric sequence
|
|
The sum of the first n terms of a finite geometric
sequence, geometric series |
|
Geometric sequences, examples
|
|
Recursive
definition and the recursion
formula |
|
|
|
|
|
|
|
Geometric sequence or
progression
|
|
A sequence of numbers in
which the ratio r
of each two successive terms an /
an
-1
is constant or whose each term is r
times the preceding.
|
|
For example, in the
sequence 1, 3, 9, 27,
. . . , each term
is 3
times the preceding,
that is r
= 3.
|
|
Therefore,
a
geometric
sequence can be written as
|
|
a1,
a2, a3, a4,
. . . , an
-1,
an, . . .
or a1,
a1 · r, a1 · r2,
a1 · r3, . . . , an
-1,
an,
. . .
|
|
where,
a2
= a1 · r,
|
|
a3 = a1 · r2,
|
|
a4 = a1 · r3,
and so on.
|
|
So,
the formula for the nth
term, or the general term of a
geometric sequence
is
|
|
|
| A
geometric sequence
is said to be convergent if -1
< r <
1 that
is,
an
approaches zero as n
becomes infinitely large thus, the limit of the sequence is 0. |
| An
infinite sequence that has no a finite limit is called a divergent
sequence. |
|
| The sum of the first n terms of a finite geometric
sequence, geometric series |
| The
sum of numbers in a geometric sequence we call the geometric series and
write, |
|
Sn = a1 + a2 + a3 +
. . .
+ an
-1 +
an, |
|
that is
Sn
= a1 + a1 · r + a1 · r2 +
. . . + a1 · rn -2
+ a1 · rn -1, |
|
or
Sn
= a1 · (1 + r + r2
+ . . . + rn -2 +
rn -1) |
| thus, |
 |
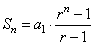the
sum of the first n terms of a finite geometric sequence or
series. |
|
| Recall
that by factoring binomial xn
-
yn
= (x
-
y) · (xn -1 +
xn -2y +
xn -3y2 +
. . .
+ xyn -2 +
y n -1) |
|
so that, rn
-
1n
= (r
-
1) · (rn -1 +
rn -2 +
rn -3 +
. . . + r2
+ r + 1). |
|
| Or,
we can use following method to derive the same formula, |
|
Sn
= a1 + a1 · r + a1 · r2 +
. . . + a1 · rn -2
+ a1 · rn -1, |
|
and
r · Sn
= a1 · r + a1 · r2
+ a1 · r3 + . . . + a1 · rn -1
+ a1 · rn, |
|
then r ·
Sn
-
Sn
= a1 · rn
-
a1
or
Sn ·
(r
-
1)
= a1 · (rn
-
1)
=> Sn
=
a1 · (rn
-
1) /
(r
-
1). |
|
| Geometric sequences examples
|
| Example:
Find
the sum of the
first six terms of the geometric sequence 1, 3, 9, 27, 81, 243, 729,
. . .
|
|
Solution: Since,
a1
= 1, r
= 3 and
n
= 6
|
|
we plug
these values into the formula for the first n
terms of a finite geometric sequence,
|
|
Sn
= [a1 · (rn
-
1)] / (r
-
1)
= [1
· (36
-
1)] / (3
-
1)
= 728 / 2
= 364.
|
|
| Example:
Find
the first term a1
and the number of
terms n
in a geometric sequence
with the general term
an
= 192, the sum
of the first n
terms Sn
=
381 and
the common ratio r
= 2.
|
|
Solution: Using
the formulas for an
and Sn
we get the system of two equations in two unknown,
|
 |
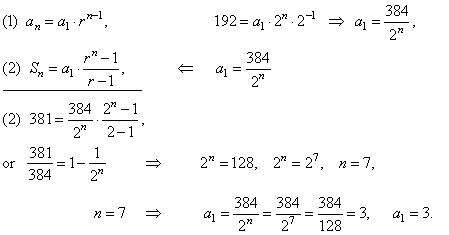| Therefore,
the geometric sequence is 3, 6, 12, 24, 48, 96, 192,
. . .
|
|
| Example:
Write the geometric
sequence such that the sum of its first three terms is 21 and the
difference between the first and the second term is 12. |
|
Solution: Given
are the equations,
|
|
(1) a1 + a2 + a3
= 21
or a1 + a1r + a1r2
= 21, a1 ·
(1 + r + r2)
= 21 |
| and
(2)
a1 -
a2
=
12
a1 - a1r
=
12,
a1 ·
(1 -
r)
= 12 |
 |
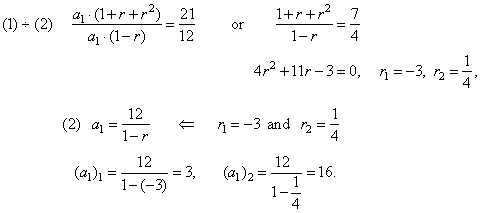| Thus,
the two geometric sequences satisfy the given conditions, |
|
(a1)1 = 3
and r1
= -3
give 3, -9,
27 |
|
(a1)2
= 16
and r2
= 1/4
give 16, 4,
1. |
|
| Example:
In a geometric
sequence the first term a1
= 3,
the general term an
= 729 and the sum
Sn
= 1092.
Find the common ratio r
and the number of terms
n.
|
|
Solution: Plug
the given values into the formulas for an
and Sn,
|
 |
|
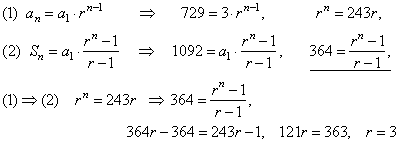(1) rn
= 243r
Ü r
= 3 |
|
3n
= 243 ·
3,
3n
= 729,
3n
= 36
Þ
n
= 6 |
| The geometric sequence is
3, 9, 27, 81, 243, 729, 2187,
. . .
|
|
| Example:
Find the first term a1,
the common ratio r
and the number of terms n
of a geometric sequence if given a6 -
a4
= 24,
a4 + a3
= 12 and
Sn
= 511. |
|
Solution:
(1) a6 -
a4
= 24,
a1r5 -
a1r3
= 24,
a1r3 · (r2 -
1)
= 24
|
|
(2) a4 + a3
= 12,
a1r3 +
a1r2
= 12,
a1r2 · (r +
1)
= 12 |
 |
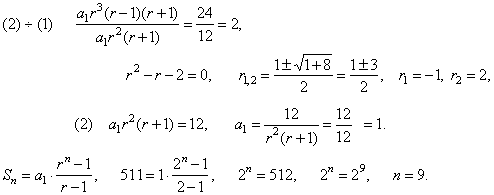| The geometric sequence is
1, 2, 4, 8, 16, 32, 64, 128, 256,
. . .
|
|
| Example:
In a geometric sequence, the difference between the fifth and the third
term relates to the
difference between the third and the second term as
12 : 1. The sum of the first three terms is 65. Find the geometric
sequence.
|
|
Solution: (1) (a5 -
a3) : (a3 -
a2) =
12
: 1
or
(a1r4 -
a1r2) / (a1r2 -
a1r) =
12,
|
 |
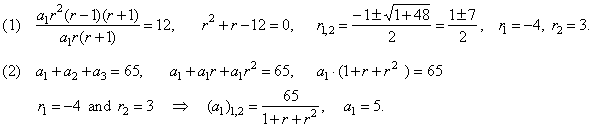| Thus,
the two geometric sequences satisfy the given conditions, |
|
a1 = 5
and r1
=
-4
give 5, -20,
80, -320,
1280, -5120,
. . . |
|
a1 = 5
and r2
=
3
give 5, 15, 45, 135, 405, 1215,
. . . . |
|
| Recursive
definition and the recursion
formula |
| A
recursion formula is the part of a recursive definition. |
| Recursive
definition is the definition of a sequence by specifying its
first term and the pattern or algorithm by which each term of the
sequence is generated from the preceding. |
| That
is, a recursion formula
shows how each term of the sequence relates to the preceding term. |
| For
example, given the first term |
|
a1
= 3
and the recursion formula, an
= an -
1 + 4,
where an
-
an -
1
= d,
d
= 4 |
| specifies
the successive terms of the arithmetic
sequence 3, 7, 11, 15, 19, 23, 27,
. . .
|
|
| Example:
Write the first five
terms of the sequence if, a1
= 7
and an
= 2an -
1 -
3. |
|
Solution: Multiply
the preceding term by 2 and subtract 3, obtained is the sequence 7,
11, 19, 35, 67, . . .
|
|
|
|
|
|
|
|
|
|
|
|
Pre-calculus contents
K
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
