|
|
Analytic Geometry (Coordinate Geometry) in Three-dimensional Space |
|
|
Line
and Plane
|
|
Point,
Line and Plane - orthogonal
projections, distances, perpendicularity of line and plane
|
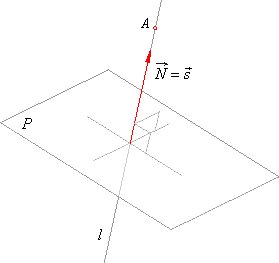
 Through a given point pass a line perpendicular to a given plane
Through a given point pass a line perpendicular to a given plane
|
 Given a line and a point, through
the point lay a plane perpendicular to the line
Given a line and a point, through
the point lay a plane perpendicular to the line
|
|
|
|
|
|
|
|
|
Point,
line and plane – orthogonal
projections, distances, perpendicularity of line and plane
|
| Through a given point pass a line perpendicular to a given plane |
| In this case, the normal vector
N
of a plane is
collinear or coincide
with the direction vector |
| s =
ai + bj + ck
of a line, |
| that is,
s =
N =
Ai + Bj + Ck. |
| The given point
A(x0,
y0,
z0)
plugged into rewritten
equation of the line gives |
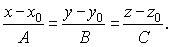 |
|
 |
|
|
|
| Example:
Determine the equation of a line which passes through
the point A(-3, 5,
-1) perpendicular to the
plane 2x -
y + 4z - 3 =
0.
|
| Solution: By
plugging the point A(-3, 5,
-1)
and the components of the normal vector
|
|
N =
s
= 2i -
j + 4k
of the given plane into
the above equation of the line obtained is
|
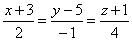
|
|
|
|
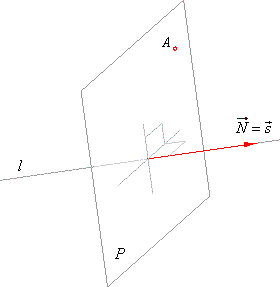
Given a line and a point, through
the point lay a plane perpendicular to the line
|
| The direction vector
s
of a line is now collinear or coincide
with
the normal vector N of a plane
so that |
| N =
s =
ai + bj + ck. |
| Coordinates of the given point
A(x0,
y0,
z0)
is plugged into the
rewritten equation
of a plane |
| P
::
a · x0 + b · y0 + c · z0 + D = 0 |
| to determine the parameter
D. |
|
 |
|
|
|
| Example:
Given is a line |
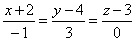 |
and a point
A(-2, 1,
4), through the point lay a plane
|
|
| perpendicular to the line. |
| Solution: In the above equation of the line, the zero in the denominator denotes that the direction
vector's
component c =
0, it does not mean division by zero. Consider this as symbolic
notation.
|
|
It means that the given line is parallel with the
xy coordinate plane on the distance
z = 3 that is, the coordinate
z
of each point of the line has the value 3.
|
|
Since N =
s
then, N =
-i
+ 3j
or
N =
Ai + Bj + Ck.
|
|
The coordinate of the point must satisfy the equation of the plane
Ax + By + Cz +
D = 0
that is,
|
|
A(-2, 1,
4) => Ax + By + Cz + D = 0
gives -1 · (-2)
+ 3 · 1
+ 0 · 4 +
D = 0, D =
-5.
|
|
Therefore, P
:: -2x +
3y -
5 = 0 is the plane through the given point perpendicular to the given line.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
J |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |