|
| A
revealing insight into the polynomial function |
|
|
|
|
|
|
|
| The principle provides full control over the polynomial |
| Hence, by
substituting coordinates of translations into the source
polynomial function we can move its graph to any desired
position on the coordinate plane. |
| Since an nth
degree polynomial with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear factors of the form (x
- ri),
where ri
denotes its real root and/or complex root |
| f
(x)
= anxn
+ an -
1xn
-
1
+
. . . +
a1x
+ a0
= an(x
- r1)(x
- r2)
. . . (x
- rn), |
| the above expression shows
following coefficients and roots relations called Vieta's
formulas. |
| Therefore, if the leading coefficient an
= 1,
we can write for
example, |
| the quadratic
polynomial by roots |
| f
(x)
= x2
+ a1x
+ a0
= (x
- r1)(x
- r2)
=
x2
- (r1
+ r2)x
+ r1r2, |
| the
cubic polynomial |
| f
(x)
= x3
+
a2x2
+ a1x
+ a0
= (x
- r1)(x
- r2)(x
- r3)
or |
| f
(x) =
x3
- (r1
+ r2
+ r3)x2
+ (r1r2
+ r1r3
+ r2r3)x
- r1r2r3, |
| the quartic polynomial |
| f
(x)
= x4
+
a3x3
+
a2x2
+ a1x
+ a0
= (x
- r1)(x
- r2)(x
- r3)(x
- r4)
or |
|
f (x) =
x4
- (r1
+ r2
+ r3
+ r4)x3
+ (r1r2
+ r1r3
+ r1r4
+ r2r3
+ r2r4
+ r3r4)x2
- |
|
- (r1r2r3
+ r1r2r4
+ r1r3r4
+ r2r3r4)x
+ r1r2r3r4, |
| and so on. |
| Note that the coefficients of a polynomial are expressed as the
alternating sums
of corresponding combinations of
products of roots. |
| Example: Find the
fifth degree polynomial (or quintic) whose roots are, |
| r1
= -
1,
r2
= -
0.5, r3
= 1, r4
= 1 and r5
= 3, |
| assuming its
leading coefficient a5
= 1, and find its source
function and draw their graphs. |
| Then, move given
function horizontally by xt
= -
3
and draw the graph
of the translated quintic function. |
| Solution:
Let's calculate coefficients of the quintic function using Vieta's
formulas, |
|
a4
= -
(r1
+ r2 + r3 + r4
+ r5)
= -
3.5 |
|
a3
= r1r2 + r1r3
+ r1r4 + r1r5
+ r2r3 + r2r4
+ r2r5 + r3r4
+ r3r5 + r4r5
= 0 |
|
a2
= -
(r1r2r3
+ r1r2r4
+ r1r2r5
+ r1r3r4
+ r1r3r5
+ r1r4r5
+ r2r3r4
+ r2r3r5
+ r2r4r5
+ r3r4r5)
= 5 |
|
a1
= r1r2r3r4
+ r1r2r3r5
+ r1r2r4r5
+ r1r3r4r5
+ r2r3r4r5
= -
1 |
|
a0
= -
r1r2r3r4r5
= -
1.5. |
| Therefore, the given
quintic function
y
= x5
-
3.5x4
+
5x2
-
x
-
1.5
is the variant -
f (-x)
of |
| f
(x)
= x5
+
3.5x4
-
5x2
-
x
+
1.5. |
| To
find the coefficients a
of the source quintic polynomial |
| fs(x)
=
a5x5
+ a3x3
+ a2x2
+ a1x |
| we can alternatively
use
the second method, through direct formula introduced above. |
| Thus, we should first
evaluate the three successive derivatives of the given quintic
at
x0,
divide each value by the corresponding factorial to obtain the
three successive coefficients. |
| Since, |
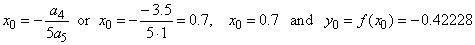 |
then, |
|
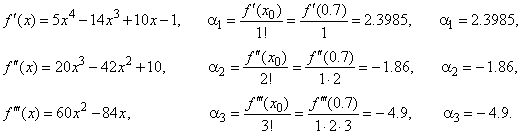 |
| Therefore, the
source quintic function
fs(x)
= x5
-
4.9x3
-
1.86x2
+ 2.3985x. |
| To translate given
quintic function in the direction of
the x-axis
by xt
= -
3, substitute each x
in its expression with (x
+
3),
(what is the same as moving
its source function by xt
= -
2.3 and
yt
= y0 = -
0.42228). |
| So,
y
= x5
-
3.5x4
+
5x2
-
x
-
1.5
gives
y
= (x
+
3)5
-
3.5(x
+
3)4
+
5(x
+
3)2
-
(x
+
3)
-
1.5 |
| or
y
= x5
+
11.5x4
+
48x3
+
86x2
+
56x,
as shows the below figure. |
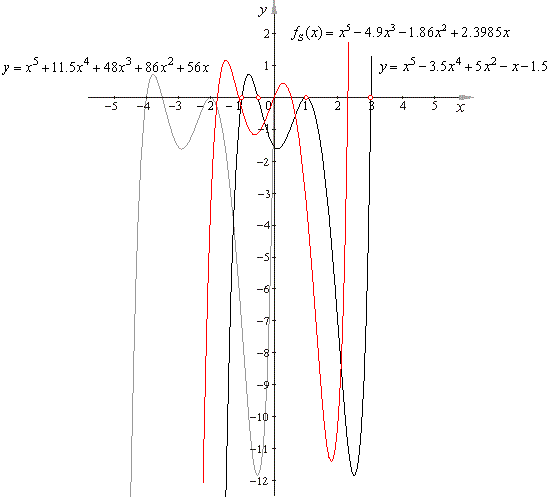 |
|
|
|
|
|
|
| *
For additional information the author invites an interested
visitor to visit the Register
page |
|
|
|
|
|
|
|
|
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |