|
|
|
|
Polynomial and/or Polynomial
Functions and Equations |
 Definition
of a polynomial or polynomial
function
Definition
of a polynomial or polynomial
function |
|
Source or original polynomial function |
|
Translating (parallel shifting) of the polynomial function |
|
Coordinates of translations and their role in the polynomial
expression |
|
Transformations of the polynomial function applied to the
quadratic and cubic functions |
|
|
|
|
|
|
| Definition
of a polynomial or polynomial function |
| A
polynomial and/or polynomial function in the variable x
is an expression of the general (or standard) form |
| f
(x)
= anxn
+ an-1xn-1
+
. . . +
a1x
+ a0 |
| consisting
of n
+ 1 terms each of which is a product of a real coefficient ai
and the variable x
raised to a non-negative
integral power. |
| If
the leading coefficient of a polynomial an is
not 0
then, the
degree of the polynomial is n. |
|
The constant term a0
is the y-intercept
of the polynomial. |
|
| Source
or original polynomial function |
| Any
polynomial f
(x)
of degree n >
1 in the general form, consisting
of n
+ 1 terms, shown graphically, |
|
represents translation of its
source (original) function in the direction of the coordinate
axes. |
|
|
The source polynomial function |
|
fs(x)
= anxn
+ an-2xn-2
+
. . . +
a2x2
+ a1x
|
|
|
| has
n
- 1 terms
lacking second and the constant term, since its coefficients, an-1
=
0
and a0
=
0
while
the leading coefficient an,
remains unchanged. |
| Therefore,
the source polynomial function passes through the
origin. |
| A
coefficient ai
of
the source function is expressed by the coefficients of the general
form. |
|
| Translating
(parallel shifting) of the polynomial function |
| Thus,
to obtain the graph of a given polynomial function f(x)
we translate (parallel shift)
the
graph of its source
function in the direction of the x-axis
by x0
and in the direction of the y-axis
by y0. |
| Inversely,
to put a given graph of the polynomial function beck to the
origin, we translate it in the opposite direction, by taking the
values of the
coordinates of translations with opposite sign. |
|
| Coordinates of translations
and their role in the polynomial expression |
| The
coordinates of translations we calculate using the formulas, |
|
|
| Hence,
by plugging the coordinates of translations into
the source polynomial function fs(x),
i.e., |
|
y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+
. . . +
a2(x
- x0)2
+ a1(x
- x0) |
|
|
| and
by expanding above expression we get the polynomial function in
the general form. |
| Inversely, by plugging the coordinates of translations into a given polynomial function
f(x), that is expressed in the general form,
i.e., |
|
y
+ y0
= an(x
+ x0)n
+ an-1(x
+ x0)n-1
+
. . . +
a1(x
+ x0)
+
a0 |
|
|
| and
after expanding and reducing above expression we get its source polynomial function. |
| Note
that in the above expression the signs of
the coordinates of translations are already changed. |
| Therefore,
each polynomial missing only second term (an-1
=
0),
represents the source polynomial whose graph is
translated in the direction of the y-axis
by
y0
= a0. |
|
| Transformations of the polynomial function
applied to the quadratic and cubic functions |
| The
application of the above theory to the quadratic and cubic
polynomial functions. |
|
| Quadratic
function f
(x)
=
a2x2
+ a1x
+ a0 |
| 1)
Let calculate the
coordinates of translations of quadratic function using the
formulas, |
| substitute
n
= 2 in |
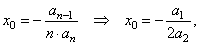 |
|
|
| then |
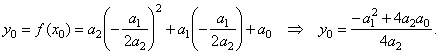 |
|
|
|
|
| 2)
To
get the source quadratic function we should plug the coordinates
of translations (with changed signs) |
|
into the general form
of the quadratic,
i.e., |
 |
| after
expanding and reducing obtained is |
|
y
=
a2x2
the source quadratic function |
|
|
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
|
y
-
y0
= a2(x
-
x0)2, |
|
|
| and
after
expanding and reducing we obtain |
|
y
=
a2x2
+ a1x
+ a0 the quadratic function
in the general form. |
|
| Cubic
function f
(x)
= a3x3
+
a2x2
+ a1x
+ a0 |
| Applying
the same method we can examine the third degree polynomial
called cubic function. |
|
| 1)
Calculate the
coordinates of translations |
| substitute
n
= 3
in |
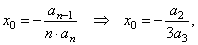 |
|
|
| then |
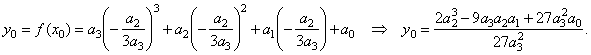 |
|
|
| 2)
To
get the source cubic function we should plug the coordinates
of translations (with changed signs) |
| into the general form
of the cubic,
i.e., |
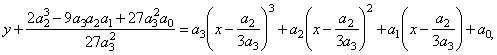 |
| after
expanding and reducing obtained is |
| |
 |
the source
cubic function. |
|
|
| 3)
Inversely, by plugging the coordinates of translations into the source
cubic |
|
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
|
|
|
after
expanding and reducing we obtain |
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 the cubic function
in the general form. |
|
| According to mathematical induction we can examine any
n-degree polynomial function using shown method. |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |