|
|
Age problems |
| Example:
A father is 48 years old
and his son is 14. |
|
a) In how many years will the father be three times older
then his son? |
|
b) How many years before was the father seven times older
then his son? |
| Solution:
After x
years a) 48
+ x = 3 ·
(14 + x) |
|
48 + x = 42 + 3x |
|
x -
3x = 42 -
48 |
|
-2x
= -6
| ¸
(-2) |
|
x = 3 years. |
|
|
Before x
years b) 48
-
x = 7 · (14 -
x) |
|
48 -
x = 98 -
7x |
|
7x -
x = 98 -
48
|
|
6x = 50
|
|
x = 25/3 = 8 years and 4
months.
|
|
|
|
Miscellaneous word
problems
|
|
Example:
If fresh grapes contain 90% water and dried 12%, how much dry grapes we get from 22 kg of fresh
|
|
grapes?
|
|
Solution: Fresh grapes contain 90% water and 10% dry substance.
|
|
Dry grapes contain 12% water and 88% dry substance.
|
| 22 kg of fresh grapes = x kg
of dry grapes, so |
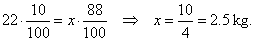 |
|
|
|
|
Example: An amount decreased 20% and then increased 50%, what is the total increase in relation to initial
|
|
value.
|
|
Solution: An initial amount
x decreased by 20%, |
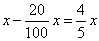 |
|
|
The obtained amount increased by 50%, |
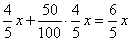 |
|
|
The difference in relation to the initial value x,
|
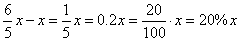 |
|
|
shows increase by 20%.
|
|
|
|
Example: From a total deducted is 5% for expenses and the remainder is equally divided to three persons.
|
|
What was the total
if each person gets $190?
|
|
Solution: If
x
denotes the total then |
 |
|
|
|
|
|
|
Example: Into 10 liters of the liquid
A poured is 4 liters of the liquid
B
and 6 liters of the liquid
C.
|
|
From obtained mixture D
poured is out 3 liters, how many liters of the liquid C
remains in the mixture
D?
|
|
Solution: A
+ B
+ C
= D
=> 10 l + 4 l + 6 l = 20 l
|
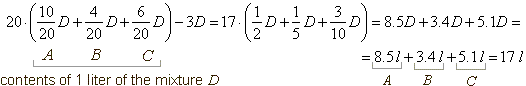
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |