|
| Trigonometry |
|
|
Trigonometric
Equations |
Homogeneous
Equations in sin
x and cos
x |
|
Homogeneous
equations of first degree a×sin x
+ b×cos
x = 0 |
|
Homogeneous
equations of second degree a
sin2
x
+ b sin x
· cos
x + c
cos2
x = 0
|
|
The
Basic Strategy for Solving Trigonometric Equations |
|
Trigonometric
equations examples |
|
|
|
|
|
|
|
| Homogeneous equations
in sin
x and cos
x |
| An equation is said to be homogeneous if all its terms are of the same degree.
|
| Homogeneous equations
of first degree a sin x
+ b
cos
x = 0 |
| Divide given equation by
cos x to obtain |
| a
tan x + b =
0 or
tan
x = -
b/a
the basic equation
|
| whose solution is
x =
tan-1
(-
b/a) + k · p
or x
= arctan
(-
b/a) + k · p,
k Î Z. |
|
|
Example: Solve the equation,
-
sin x
+
Ö3
· cos x = 0.
|
|
Solution: Dividing given equation by
-
cos x
obtained is
|
| tan
x =
Ö3,
x =
tan-1Ö3
+ k · p =
p/3
+ k · p,
k Î Z. |
|
| Homogeneous equations
of second degree a
sin2
x
+ b sin x
· cos
x + c
cos2
x = 0 |
| After division of the given equation by
cos2
x obtained is quadratic
equation |
| a
tan2
x
+ b tan x + c = 0 |
| which is
explained in the previous section. |
|
| The
next example shows that the equation a
sin2
x
+ b sin x
· cos
x + c
cos2
x = d
is also homogeneous. |
|
|
Example: Find the solution set for the equation,
5
sin2
x
+ sin x · cos
x + 2
cos2
x = 4.
|
|
Solution: Given equation is equivalent to the equation
|
| 5
sin2
x
+ sin x · cos
x + 2
cos2
x = 4
· (sin2
x
+ cos2
x),
since sin2
x
+ cos2
x = 1 |
| which,
when simplified becomes |
| sin2
x
+ sin x · cos
x - 2
cos2
x = 0
- the homogeneous equation of the second degree. |
| Division by cos2
x
gives, |
 |
|
|
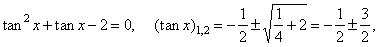thus, (tan x)1
= - 2,
x =
tan-1(- 2)
= -
63°26′05″ + k · 180°, |
|
(tan x)2
= 1,
x′ =
tan-1
1
= 45° + k · 180°,
k Î Z. |
|
| The
basic strategy for solving trigonometric equations |
| When solving trigonometric equations we usually use some of the following
procedures, |
| - apply known
identities to modify given equation to an equivalent expressed in terms of one function, |
| - rearrange the given
equation using different trigonometric formulae to an equivalent, until you recognize one |
|
of the known types. |
|
| Trigonometric equations
examples |
|
Example: Solve the equation,
3
sin
(x
+ 70°) + 5
sin
(x
+ 160°) = 0.
|
|
Solution: Given equation
can be written as
|
| 4
sin
(x
+ 70°) - sin
(x
+ 70°) + 4
sin
(x
+ 160°)
+ sin
(x
+ 160°) = 0 |
|
or 4
[sin
(x
+ 70°)
+ sin
(x
+ 160°)] =
sin
(x
+ 70°) - sin
(x
+ 160°) |
 |
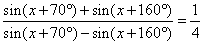| then, by using sum to product formula
|
|
|
|
cot
(- 45°) · tan
(x
+ 115°) = 1/4
or tan
(x
+ 115°) = - 1/4,
|
| therefore,
the solution x
+ 115° = tan-1
, x =
-115°
+ tan-1
(-1/4) =
- 129°2′10″ + k · 180°. |
|
|
Example: Find the solution
of the equation, 2
sin
(x
+ 60°) · cos
x = 1.
|
|
Solution: Applying products as sums formula
|
| 2 · (1/2)
[sin
(x
+ 60°
+ x)
+ sin
(x
+ 60° - x)] = 1
or sin
(2x
+ 60°)
+ sin 60° = 1
|
| then
sin
(2x
+ 60°) = 1
- Ö3/2,
2x
+ 60° =
sin-1(1
- Ö3/2) + k · 360° |
|
and 2x′
+ 60° =
180°
- sin-1(1
- Ö3/2) + k · 360° |
| so,
the solution is 2x =
-
60°
+ sin-1(1
- Ö3/2) + k · 360°,
x =
-
26°9′1″ + k · 180°, |
|
2x′ =
120° - sin-1(1
- Ö3/2) + k · 360°,
x′ = 56°9′1″ + k · 180°,
k Î Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
