|
| Trigonometry |
|
|
Trigonometric
Equations |
Equations
that Can be Written as f
· g = 0 |
|
Trigonometric
Equations of Quadratic Form |
|
The
Basic Strategy for Solving Trigonometric Equations |
|
Trigonometric
equations examples |
|
|
|
|
|
|
|
| Trigonometric
equations that can be
written as f
· g = 0 |
| If the given equation, by using appropriate transformations, can be rearranged to the form
f · g = 0 then its
solution is represented as the union of the individual solutions of the equations
f = 0 and
g = 0. |
|
|
Example: Solve the equation,
sin (x +
30°) + sin
(30° -
x) = 2cos2 x.
|
|
Solution: Using the sum to product formula (or addition formula)
|
 |
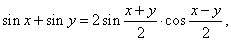| given equation gets the form |
 |
|
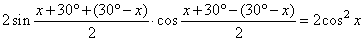that is, 2sin
30° · cos x = 2cos2 x |
|
or cos
x -
2cos2 x = 0,
cos x · (1 -
2cos x) = 0
the equation of the form f
· g = 0 |
|
therefore, cos
x = 0,
x = 90° + k · 180°, kÎ Z, |
|
and 1 -
2cos x = 0,
cos x = 1/2, x = +
60° + k · 360°, kÎ Z. |
| Thus, the solution set of the given equation
we can write as |
| {90° + k · 180° : kÎ
Z} U {+
60° + k · 360° : kÎ
Z} or {90° + k · 180°, +
60° + k · 360° : kÎ
Z}. |
|
| Trigonometric
equations of quadratic form |
| The trigonometric equation of the quadratic form
[F (x)]2
+ p · F (x) + q = 0, |
| where
F (x)
denotes given trigonometric function, by substituting F
(x) = u becomes a quadratic equation |
 |
| returned into substitutions
F
(x) = u1
and F
(x) = u2
lead to the known basic trigonometric equation. |
|
|
Example: Find the solution set for the equation,
3sin x = 2cos2
x.
|
|
Solution: Using known identity
we write 3sin
x -
2 · (1 -
sin2 x) = 0,
and by plugging
sin x =
u
|
 |
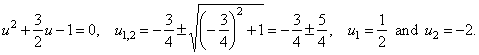| Therefore,
sin x =
1/2,
x = 30° + k · 360°, kÎ Z,
and x′ = 150° + k · 360°, kÎ Z, |
| while the equation
sin x =
-
2 has no solutions since
-
2 is not in the range of the sine function. |
| Thus,
the solution set of the given equation is {30° + k · 360°, 150° + k · 360° : kÎ
Z}. |
|
| The
basic strategy for solving trigonometric equations |
| When solving trigonometric equations we usually use some of the following
procedures, |
| - apply known
identities to modify given equation to an equivalent expressed in terms of one function, |
| - rearrange the given
equation using different trigonometric formulae to an equivalent, until you recognize one |
|
of the known types. |
|
| Trigonometric equations
examples |
|
Example: Solve the equation,
3
sin
(x
+ 70°) + 5
sin
(x
+ 160°) = 0.
|
|
Solution: Given equation
can be written as
|
| 4
sin
(x
+ 70°) - sin
(x
+ 70°) + 4
sin
(x
+ 160°)
+ sin
(x
+ 160°) = 0 |
|
or 4
[sin
(x
+ 70°)
+ sin
(x
+ 160°)] =
sin
(x
+ 70°) - sin
(x
+ 160°) |
 |
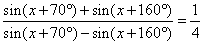| then, by using sum to product formula
|
|
|
|
cot
(- 45°) · tan
(x
+ 115°) = 1/4
or tan
(x
+ 115°) = - 1/4,
|
| therefore,
the solution x
+ 115° = tan-1
, x =
-115°
+ tan-1
(-1/4) =
- 129°2′10″ + k · 180°. |
|
|
Example: Find the solution
of the equation, 2
sin
(x
+ 60°) · cos
x = 1.
|
|
Solution: Applying products as sums formula
|
| 2 · (1/2)
[sin
(x
+ 60°
+ x)
+ sin
(x
+ 60° - x)] = 1
or sin
(2x
+ 60°)
+ sin 60° = 1
|
| then
sin
(2x
+ 60°) = 1
- Ö3/2,
2x
+ 60° =
sin-1(1
- Ö3/2) + k · 360° |
|
and 2x′
+ 60° =
180°
- sin-1(1
- Ö3/2) + k · 360° |
| so,
the solution is 2x =
-
60°
+ sin-1(1
- Ö3/2) + k · 360°,
x =
-
26°9′1″ + k · 180°, |
|
2x′ =
120° - sin-1(1
- Ö3/2) + k · 360°,
x′ = 56°9′1″ + k · 180°,
k Î Z. |
|
|
Example: Find the solution
of the equation, |
 |
|
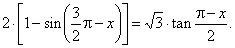| Solution: Using
identities |
 |
|
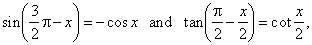| given
equation becomes 2 · (1
+ cos x) - Ö3
· cot x/2 = 0, |
 |
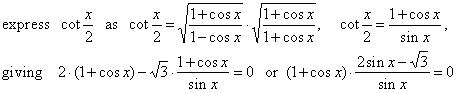| therefore,
1
+ cos x
= 0,
cos
x
= - 1,
x
= p
+ k · 2p, |
|
and 2sin
x - Ö3
= 0,
sin
x
= Ö3/2,
x
= p/3
+ k · 2p
and x′ = 2p/3
+ k · 2p,
k Î Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
