|
 Translated
cubic functions
Translated
cubic functions |
|
Translated
cubic function the type 1 - the tangent line at the point of
inflection is horizontal |
|
Translated
cubic function the type 2/1 - no turning points, the tangent at
inflection is a slant line |
|
Translated
cubic function the type 2/2 - with two turning points, the
tangent at inflection is a slant line |
|
Graphing a cubic
function type 2/1 example |
|
|
|
|
|
|
|
| Translated
cubic functions |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
where, |
|
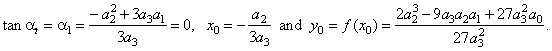 |
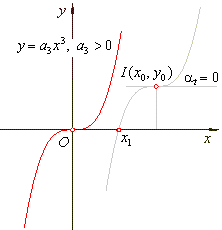 |
|
The
root |
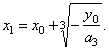 |
The point of inflection I(x0,
y0). |
|
|
|
|
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
>
0, |
|
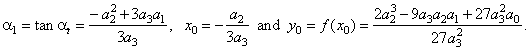 |
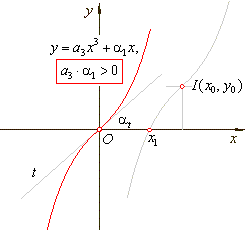 |
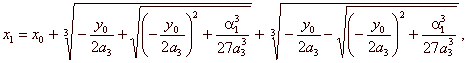 |
I(x0,
y0). |
|
|
|
|
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+ a1(x
-
x0),
a3
· a1
<
0, |
|
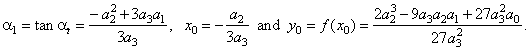 |
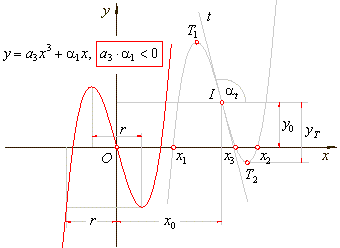 |
| If
| y0
| > | yT
| |
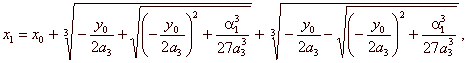 |
| if
| y0
| £
|
yT
| |
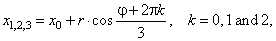 |
|
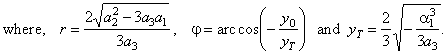 |
|
The turning points |
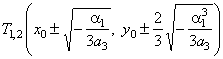 |
The
point of
inflection
I(x0,
y0). |
|
|
|
|
|
|
|
| Graphing a cubic
function type 2/1 example |
| Example:
Find the coordinates of
translations, the zero point, the point of inflection and draw
graphs of
the cubic function y
=
-
x3
+ 3x2
-
5x
+
6
and its source function. |
| Solution:
1)
Calculate the coordinates of translations
|
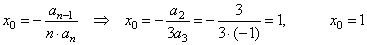 |
|
y0
= f
(x0)
Þ y0
= f (1)
=
-13
+ 3 · 12
-
5
· 1
+
6 =
3,
y0
= 3 |
| Therefore,
the point of inflection I
(1,
3). |
| 2)
To
get the source cubic function, plug the coordinates
of translations into the general
form
of the cubic, |
| y
+ y0
=
a3(x
+
x0)3
+ a2(x
+
x0)2
+ a1(x
+
x0)
+ a0 |
| thus,
y
+ 3
=
-1·
(x
+
1)3
+
3 · (x
+
1)2
-
5
· (x
+
1)
+
6 => y
=
-
x3 -
2x
the source
function. |
| Let
prove that the source cubic is an odd function, which means
that f (x)
=
- f
(-x), |
| since
f (x)
=
-
x3 -
2x
then
-
f (-x)
=
- [-
(-x)3
-
2(-x)]
=
- [
x3
+ 2x]
=
-
x3 -
2x. |
| As,
a3
=
-
1 and
a1
=
-
2
then a3a1 >
0
therefore, given function is of the type 2/1. |
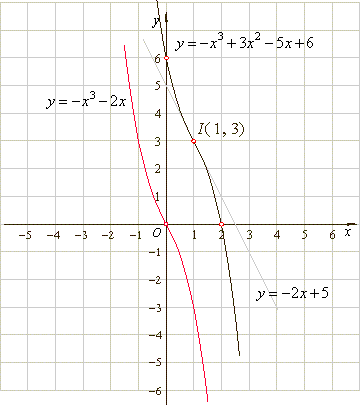
| Since given function is symmetric to its
point of inflection, and as the y-intercept
a0
=
6, then the x-intercept
or zero of the function must be at the point (2,
0) as
shows the below figure. |
| To
prove the root plug the values, a3
=
-
1,
a1
=
-
2,
x0
=
1 and
y0
=
3 into |
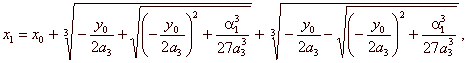 |
| so
x1
= 2, therefore
-
x3
+ 3x2
-
5x
+
6
= -1(x
-
2)(x2
-
x
+
3). |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |