 Limits of
rational functions
Limits of
rational functions |
|
Evaluating
the limit of a rational function at infinity |
|
Evaluating
the limit of a rational function at a point |
|
The limit of a rational function that is defined at the given point |
|
The limit of a rational function that is not defined at the
given point |
|
|
|
|
|
|
|
| Limits of
rational
functions |
| A
rational function is the ratio of two polynomial functions |
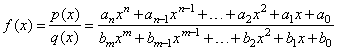 |
| where
n and m
define the degree of the numerator and the denominator
respectively. |
|
| Evaluating
the limit of a rational function at infinity |
| To
evaluate the limit of a rational function at infinity
we divide both the numerator and the denominator of
the function by the highest
power of x
of
the denominator. |
| Example: Evaluate
the limit |
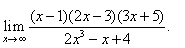 |
|
| Solution:
|
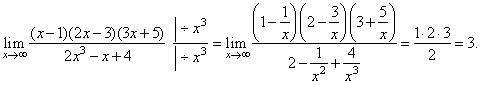 |
|
|
| Example: Evaluate
the limit |
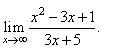 |
|
| Solution:
|
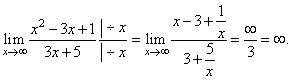 |
|
|
| Example: Evaluate
the limit |
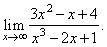 |
|
| Solution:
|
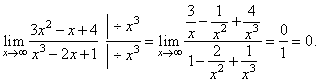 |
|
| Therefore,
the following three cases are possible; |
| 1.
If the degree of the numerator is greater than the degree of the
denominator (n
> m), then the
limit of the rational function does not exist, i.e., the
function diverges as x
approaches infinity. |
| 2.
If the degree of the numerator is equal to the degree of the
denominator (n
= m), then the limit of the rational function is
the ratio an/bm
of the leading coefficients. |
| 3.
If the degree of the numerator is less than the degree of
the denominator (n <
m), then the
limit of the rational function,
as x
tends to infinity, is zero. |
| The line
y
= c is a horizontal
asymptote of the graph of f(x)
if |
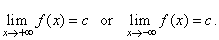 |
|
|
| Thus, a
rational function has a horizontal asymptote if the function
values tend to a constant value c as
x |
| approaches plus or minus infinity.
|
|
| Evaluating
the limit of a rational function at a point |
| A
rational function is continuous at every x
except for the zeros of the denominator. |
| Therefore,
all real numbers
x
except for the zeros of the denominator, is the domain of a rational function. |
| The
zeros of the numerator that are in the domain are the x-intercepts
or roots of a rational function. |
| If
x
= a is
a zero of the numerator and not a zero of the denominator,
then f
(a)
= 0 or a
is the root of the rational
function. While if both the numerator and denominator are zero,
we get the indeterminate form 0/0. |
| Factoring
the numerator and denominator into irreducible factors allows us
to find all of the zeros of the numerator
and denominator. |
|
| a)
The limit of a rational function that is defined at the given point |
| Given a
rational function |
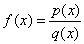 |
where p(x) and
q(x) are
polynomials, to find |
|
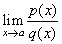 |
|
we first evaluate p(a) and
q(a)
by substituting x
= a
into both polynomials then |
| if
q(a)
¹
0
then f(x)
is continuous at a
and the limit is |
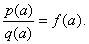 |
|
|
|
| Example: Evaluate
the limit |
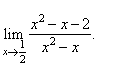 |
|
| Solution:
We first factor
the numerator and denominator |
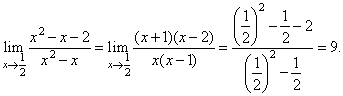 |
| Since
q(1/2)
is not 0
then |
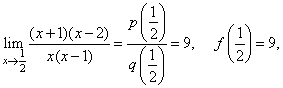 |
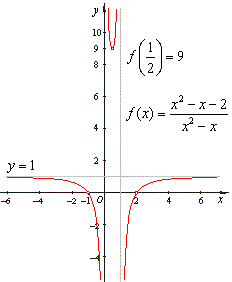
| x
= 0
and x
= 1
are vertical asymptotes, and y
= 1
is the |
| horizontal
asymptote, as is shown in the right figure. |
|
 |
|
|
| b)
The limit of a rational function that is not defined at the
given point |
| At
every point that is a zero of the denominator a rational
function has either a vertical asymptote or a hole in the
graph cased by the
indeterminate form 0/0. |
| The
vertical asymptote is called the infinite discontinuity while
the hole in the graph is called removable discontinuity
since the
indeterminate form can be avoided by canceling common factors in
the numerator and the
denominator. |
| Thus,
a point of discontinuity or hole in the graph exists when a zero
of the numerator is matched by a zero of
the
denominator and the factor occurs to the same degree in the
numerator and the denominator. |
| Given a
rational function |
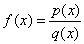 |
then, |
|
|
- if q(a)
= 0 and
p(a) is
not 0
then one-sided limits |
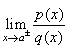 |
are
infinite limits. |
|
|
That means, the rational function has the vertical asymptote at x
= a. |
|
- if q(a)
= 0 and
p(a)
= 0
the
polynomials p(x) and
q(x)
have a common factor (x
-
a). |
|
The rational function has the removable discontinuity or the
hole in the graph at the point x
= a. |
| When
both the numerator and denominator of a rational function vanish
at the given point a,
we factor and cancel
common factors and then find the limit of the equivalent
function. |
|
| Example: Evaluate
the limit |
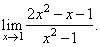 |
|
| Solution:
To avoid the indeterminate form 0/0,
the expression takes as x
®
1,
we factor and cancel common
factors |
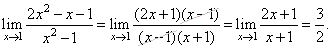 |
|
The rational function has the hole in the graph at x
= 1, |
| the vertical
asymptote
x
= -1
and
the horizontal |
| asymptote
y
= 2
since |
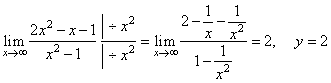 |
| as is shown in the right figure. |
|
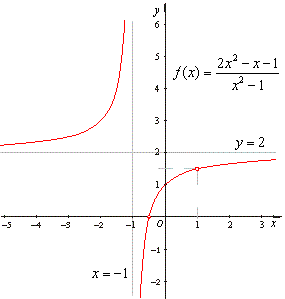 |
|
|