|
| Integral
calculus |
|
|
|
The
indefinite integral |
 Integration by parts rule
Integration by parts rule |
|
Evaluating the indefinite integrals using the integration by parts
formula, examples
|
|
Evaluating the indefinite integrals using the integration by parts
formula, solutions
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Integration
by parts rule
|
|
The rule for differentiating the
product of two differentiable functions leads to the integration
by parts formula.
|
|
Let f
(x)
and g
(x)
are differentiable functions, then the product rule gives
|
|
[ f
(x) g (x)]'
= f (x)
g (x)' + g (x)
f ' (x),
|
| by
integrating both sides |
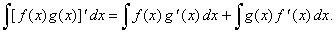
|
|
Since the integral of the derivative
of a function is the function itself, then
|
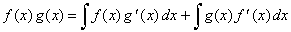
|
|
and by rearranging obtained is
|
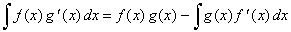
|
|
the integration by parts
formula.
|
|
By substituting
u = f
(x) and
v
= g (x)
then, du =
f ' (x)
dx and dv
= g' (x)
dx, so that
|
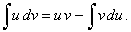
|
|
To apply the above formula, the
integrand of a given integral should represent the product of one
function and the differential of the other.
|
|
The selection of the function
u and the differential dv
should simplify the
evaluation of the remaining integral.
|
|
In some cases it will be necessary to
apply the integration by parts repeatedly to obtain a simpler
integral.
|
|
|
| Evaluating the indefinite integrals using the integration by parts
formula, examples
|
| Evaluate
the following indefinite integrals using the integration by parts
formula;
|
| 47. |
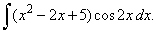 |
48. |
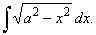 |
|
| 49. |
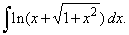 |
50. |
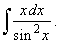 |
|
| 51. |
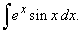 |
52. |
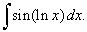 |
|
|
|
| Evaluating the indefinite integrals using the integration by parts
formula, solutions
|
| Example:
47. Evaluate |
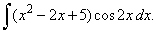 |
|
|
|
|
| Example:
48.
Evaluate |
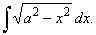 |
|
|
|
|
| Example:
49.
Evaluate |
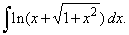 |
|
|
|
|
| Example:
50.
Evaluate |
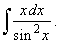 |
|
|
|
|
| Example:
51.
Evaluate |
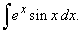 |
|
|
|
|
| Example:
52. Evaluate |
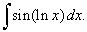 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Functions
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |