|
|
Vectors in a Plane and Space |
|
The mixed product
or the scalar triple product |
|
The mixed product
or scalar triple product definition |
|
The
mixed product properties |
|
The condition for
three vectors to be coplanar |
|
The mixed product
or scalar triple product expressed in terms of components |
|
The vector product
and the mixed product use, examples |
|
|
|
|
|
|
| The mixed product |
| The
mixed product or scalar triple product definition
|
| The
mixed product (or the scalar triple product) is the scalar product of the first vector with the vector product of the other two
vectors denoted as a
· ( b ´
c ).
|
|
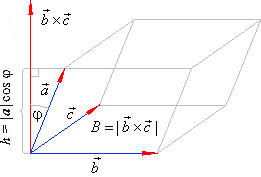
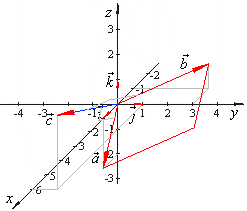
Geometrically, the
mixed product is the volume of a parallelepiped defined by vectors,
a ,
b
and c
as shows the right figure.
|
The vector b
´
c is perpendicular to the base of the
parallelepiped and its magnitude equals the area of
the
|
|
base, B =
| b ´
c
|.
|
The altitude of the parallelepiped is projection of the
vector a in the direction of
the vector
b ´
c,
so
|
|
h =
| a | · cos j.
|
|
 |
|
| Therefore, the scalar product of the vector
a
and vector
b ´
c
is equal to the volume of the parallelepiped.
|
|
|
| The sign of the scalar triple product can be either positive or negative, as
a
· ( b ´
c ) =
-
a
· ( c ´
b ).
|
|
| The
mixed product properties |
 |
|
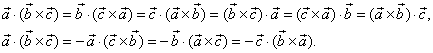| The condition for
three vectors to be coplanar |
The
mixed product is zero if any two of vectors, a ,
b
and c
are parallel, or if a ,
b
and c
are coplanar. That is,
when the given three vectors are coplanar the altitude of the parallelepiped is zero and thus the scalar triple
product is zero, |
|
|
|
| The
mixed product or scalar triple product expressed in terms of components |
| The scalar triple product expressed in terms of the components of vectors,
a =
axi + ay j + azk, |
| b
= bxi + by j +
bzk
and c
= cxi + cy j +
czk, |
|
|
| The above formula can be derived from the determinant expanded by minors through the elements of the
first row, |
 |
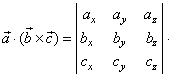| Therefore, vectors,
a,
b
and c
will be coplanar if the determinant is zero. |
|
| The vector product
and the mixed product use, examples |
| Example:
Given are vectors, a
= i -
2 k and
b =
-
i + 3 j + k, determine the vector
c
= a
´
b
and the area of a parallelogram formed by vectors, a
and b.
|
| Solution: |
 |
|
|
|
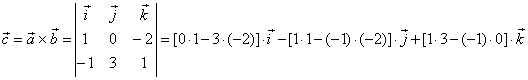| The area of the
parallelogram, |
 |
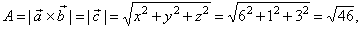| or |
 |
|
|
 |
|
|
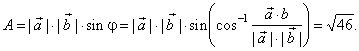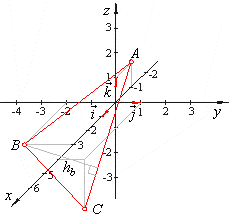
| Example:
Vertices of a triangle are, A(-1,
0, 1), B(3,
-2,
0) and C(4,
1, -2),
find the length of the altitude hb.
|
|
Solution:
Using the area of
a triangle,
|
 |
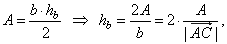| as
the area of the triangle
|
 |
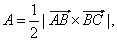where |
|
 |
|
 |
|
 |
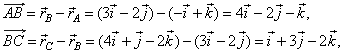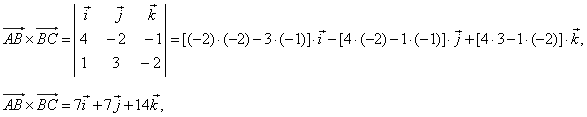| then,
the area of the triangle, |
 |
|
|
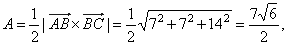| and the
length of the side b, |
 |
|
|
|
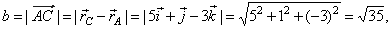| thus,
the length of the altitude, |
|
|
 |
|
|
|
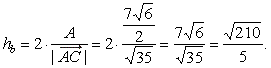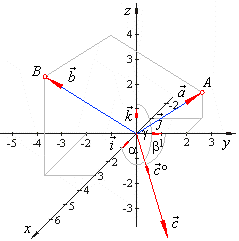
| Example: Find the angles that
the unit vector, which is orthogonal to the plane formed by vectors,
|
| a
= -i +
2 j + k
and b
= 3i -
2
j + 4k,
makes with the coordinate axes. |
|
Solution:
The unit vector which is orthogonal to the plane,
formed by the vectors, a
and b,
is the direction vector of a vector c,
such that
|
 |
|
 |
|
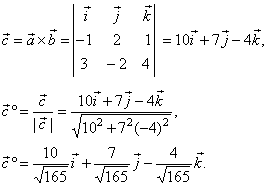| Angles, which the unit vector
c°
forms with coordinate axes, we find by using the formula, |
 |
|
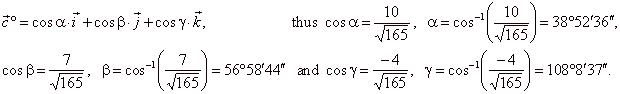| Example: Given are vectors,
a
= -2i -
3 j,
b
= -i -
2
j + 3k
and c
= -i +
2
j + k,
find the projection
(the scalar component) of the vector a
onto vector d
= b ´
c.
|
| Solution:
Let first find
the vector d, |
 |
 |
|
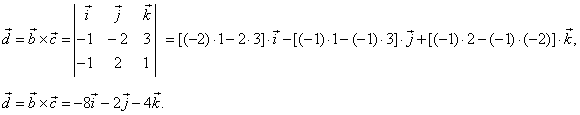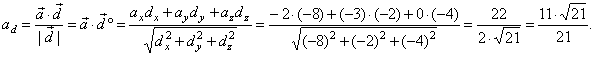