|
| Conic
Sections |
|
|
|
|
Hyperbola
and Line
|
 Hyperbola and line relationships
|
|
Construction
of tangents from a point outside the hyperbola
|
|
Properties of the hyperbola
|
|
The area of a triangle which the tangent at a point on the hyperbola forms with
asymptotes |
|
The
tangency point bisects the line segment of the tangent between
asymptotes |
|
The
parallels to the asymptotes through the tangency point intersect
asymptotes |
|
|
|
|
|
|
|
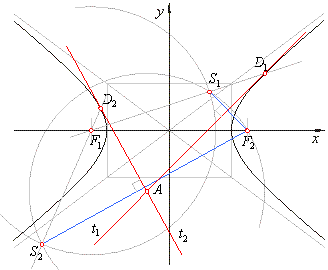
| Construction of tangents from a point outside the hyperbola |
|
With A as center draw an arc through
F2,
and from F1as center, draw an arc of radius
2a.
|
|
These arcs intersect at points
S1
and
S2.
|
|
Tangents are the
perpendicular bisectors of the line segments F2S1
and
F2S2.
|
|
Tangents can also be drawn as lines through
A and
the intersection points of lines through F1S1
and
F1S2,
with the hyperbola.
|
|
These intersections are at the same
time the points of contact
D1
and
D2.
|
|
 |
|
|
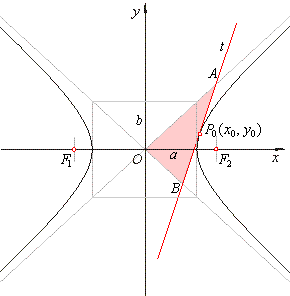
| Properties of the hyperbola
|
| -
The area of a triangle which the tangent at a point on the hyperbola forms with
asymptotes, is of constant
|
|
value A
= a ·
b. Vertices of the triangle are the origin
O
|
|
and the intersections
A and
B of the tangent to the
hyperbola at
the point P0(x0, y0)
with
asymptotes. Then,
|
|
(1) t1 ::
b2x0x
-
a2y0y
= a2b2
-the tangent
|
|
(2) y =
±
(b/a) · x
-asymptotes
|
the solution of the system of the equations
(1)
and (2)
gives intersections A and
B. Plugging
(2) into
(1)
|
|
|
|
 |
|
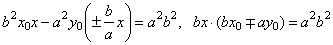
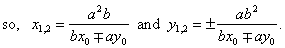
| Since one vertex of the triangle is the origin
O(0, 0) then
the formula for the area, AD=
(x2y1
-
x1y2)/2
or |
 |
|
| -
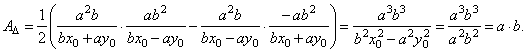The tangency point bisects the line
segment AB
of
the tangent between
asymptotes. |
|
The abscissa of the midpoint of the segment
AB,
|
|
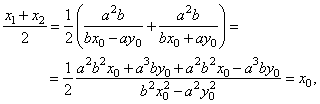
| equals
the abscissa of the tangency point.
|
|
|
|
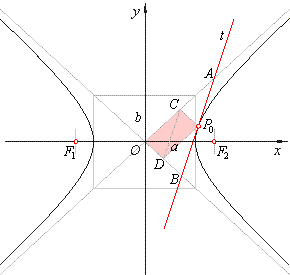
- The
parallels to the asymptotes through the tangency
point intersect asymptotes at the points,
C and
D
|
|
such
that, OC
= AC
and OD
= BD
.
|
|
 |
|
| Therefore, if given are asymptotes and the tangency point
P0,
we can construct the tangent by drawing the parallel to the asymptote
y = (b/a)
· x
through P0
to D. Mark endpoint
B
of segment OB
taking D
as the midpoint. Thus, the line segment P0B determines the tangent line. |
| On a similar way we could determine intersection
A,
of the tangent and another asymptote, using point C. |
| Since
triangles, ODC,
DP0C,
DBP0 and
CP0A,
are congruent, it follows that the area of the parallelogram
ODP0C
is equal to half of the area of the triangle
OBA,
i.e.,
A
= (a ·
b) / 2. |
|
| Using this property we can derive
the equation of the equilateral or rectangular hyperbola with the
coordinate axes as its
asymptotes.
|
As the
asymptotes of an equilateral hyperbola are
mutually perpendicular then the given parallelogram is
the rectangle.
|
| And
since the axes of the equilateral hyperbola are equal
that is a
= b,
then the area A
= a2
/ 2.
|
|
Then, for every point in the new coordinate system
|
|
|
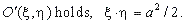
If we now change the coordinates into
x
and y,
and
denote the constant by c, obtained is
|
|
|
|
the equation
of
the
equilateral or rectangular hyperbola
with the coordinate axes as its asymptotes.
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
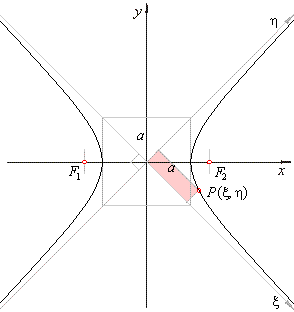| College
algebra contents E |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
