|
| Integral
calculus |
|
|
Applications
of the definite integral
|
 The
area of the sector of a curve in polar coordinates
The
area of the sector of a curve in polar coordinates
|
|
The
area of the sector of a curve given in Cartesian (or rectangular) coordinates
|
|
The
area of the sector of a parametric curve
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The
area of the sector of a curve in polar coordinates
|
|
Polar coordinates (
r, q )
locate a point in a plane by means of the length r,
of the line joining the point to the origin or pole
O,
and angle q
swept out by that line from the polar axis.
|
|
Recall the area A
of a circular sector bounded by two radii and an arc, is defined
by the proportion
|
|
A : r2
p
= q
: 2p
thus, A
= (1/2) r2q
|
|
where r
is the length of the radius and q
is the central angle subtended by the arc.
|
|
Suppose given a curve in polar
coordinates by r
= f (q
)
or r
= r
(q
)
then, the area of the region bounded by the curve and the radii that correspond to
q
1 = a
and q
2 = b,
is given by
|
|
|
|
|
|
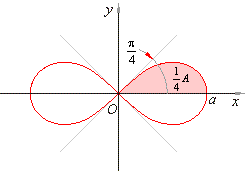
Example:
Find the area of the
region enclosed by the lemniscate of Bernoulli whose polar equation
is r2 = a2
cos2q,
shown in the below figure.
|
|
Solution: As the
lemniscate consists of two symmetrical loops meeting at a node, we will calculate quarter
of the
area lying inside 0
<
q
<
p/4.
|
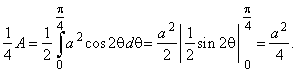 |
| Thus,
the area of the lemniscate A
= a2. |
|
 |
|
|
|
|
The
area of the sector of a curve given in Cartesian (or rectangular) coordinates
|
|
We
use the formulas for conversion between Cartesian and polar
coordinates,
|
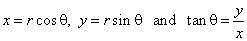
|
|
to find the area of the sector bounded by
two radii and the
arc P0P,
of a curve y
= f (x) given in the
|
|
Cartesian coordinates, where x
is the value inside the interval [a,
b]. Then
|
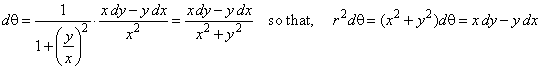
|
|
therefore,
|
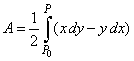
|
|
is the area of the sector bounded by
two radii and the arc P0P
of a curve y
= f (x).
|
|
|
|
The
area of the sector of a parametric curve
|
|
The area of the sector bounded by two
radii and the arc P0P
of a parametric curve is given by
|
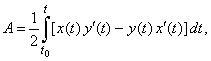
|
|
where the parametric values, t0
and t
relate to the endpoints, P0
and P
of the arc, respectively.
|
|
|
|
Example:
Find the area of the
sector of the rectangular hyperbola x2
-
y2 = 1
enclosed by the
x-axis, the arc of the right branch of the
hyperbola between the vertex and the point
P(cosh
t,
sinh
t), and the
line joining this point to the origin, as shown in
the below figure.
|
|
Solution: Since the hyperbolic functions satisfy the identity
cosh2
t
-
sinh2
t = 1 then, the point
x = cosh
t and
y = sinh
t
that lies on the
hyperbola x2
-
y2 = 1,
describes the right branch of the
hyperbola as parameter
t increases from
-
oo
to +
oo.
|
|
The point traces the hyperbola passing from negative infinity, through
P0
(t = 0) to positive
infinity.
|
| As,
x'
(t) = sinh
t
and
y' (t) = cosh
t, |
| so
that x(t)
y' (t) = cosh2
t
and
y(t) x' (t) = sinh2
t, |
| and
by using the above formula for the area of the
sector |
| of
a parametric curve |
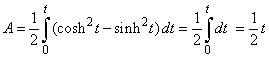 |
| we
get the area of the sector P0OP
of the rectangular hyperbola. |
|
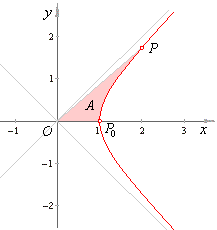 |
|
|
Therefore, the parameter (or argument)
t,
of hyperbolic functions, is twice the area of the sector P0OP,
i.e., t = 2A.
That is why the inverse hyperbolic functions are also called the
area functions.
|
|
|
|
The
area between two curves
|
|
If
given are two continuous functions, f
and g
defined over an interval [a,
b],
with g
(x)
<
f (x)
for all x
in
[a,
b],
then the area A
of the region bounded (or enclosed) by these two curves and the
lines x
= a
and
x
= b
is
given by
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Calculus contents
F |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |