|
| Integral
calculus |
|
|
|
 The indefinite integral applications
The indefinite integral applications |
|
Kinetic equation of free fall |
|
Exponential
growth and decay (increase and decrease) |
|
|
|
|
|
|
|
| The
indefinite integral applications |
| In
physics, physical laws are described by mathematical formulas. |
|
| Kinetic
equation of free fall |
| For
example kinetic quantity velocity v, defined as the rate at which position
s
changes with respect to time t, |
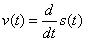 |
| represents
an antiderivative or primitive function of v
(t), hence |
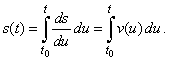 |
| Since,
at t = t0,
the formula for displacement gives s(t0)
= 0 then, the constant t0
denotes the point in time when
starts measurement of the displacement. |
| Thus
for example, the velocity of an object in free fall motion |
| v
= gt, |
| where
g = 9,81 m/s/s is
the acceleration of free fall (the acceleration due to gravity),
therefore the displacement |
| |
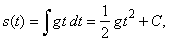 |
| what
can be checked over by differentiating the right-hand side with respect
to t
to obtain the integrand
gt.
|
|
|
Exponential growth and decay (increase and decrease) |
| A
quantity that increases or decreases with respect to
time t, or other
argument,
such that the rate of change by
which it happens at an instant t
is proportional by the value of the quantity at that instant, then it changes
by the exponential law. |
| Let
x (t)
denotes the value of a quantity at a time t,
the rate dx/dt,
at which the quantity changes at
an instant t
is proportional
by the value of the quantity at that instant, with constant of
proportionality k
then, x (t) satisfies
the differential equation of the exponential function |
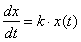 |
| where
the sign of constant of proportionality k
depends
on whether x(t)
increases or decreases with t. |
| To
solve the above differential equation we rewrite it by multiplying
by dt
and dividing by x(t)
to separate variables so that each side of the equation
can be integrated with respect to each variable, |
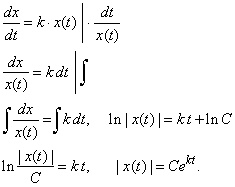 |
| By
setting t
= 0 to both sides of
the solution gives |
x(0) | = C
thus,
the constant of integration defines the
initial value of the quantity
| x(t)
|. |
|
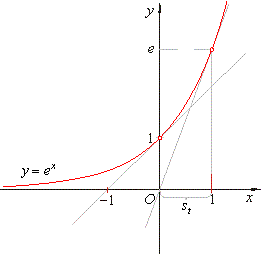 |
|
| Therefore,
the general solution of the differential
equation |
| dx/dt
= k ·
x
(t) |
| is
represented by the exponential function multiplied by an arbitrary
constant x (0), |
| x
(t)
= x (0)
ekt |
|
or y
(t)
= C
ekt
is a solution to the differential equation dy/dt
= k
y. |
| Recall
that the graph of the
exponential function f
(x)
= ex and
its derivative
coincide, i.e., |
| y'
= dy/dx = ex
= y |
| so
that the sub tangent (projection of the segment of the tangent onto the x-axis)
drawn at any point x, |
| st
=
y
/ y'
=
1, |
| as
is shown in the above figure. |
| Therefore,
for x(0) >
0 and k
> 0,
the quantity x(t)
increases as t
increases while, in case the coefficient of t
is negative, i.e., k
< 0,
x(t)
decreases, for which an example is radioactive decay. In this case the graph
of the exponential function reflects around the y-axis. |
|
|
|
|
|