Coordinate Geometry (Analytic Geometry) in Three-dimensional Space
     Line and Plane
      Projection of a point onto a plane
      Projection of a point onto a line
Projection of a point onto a plane
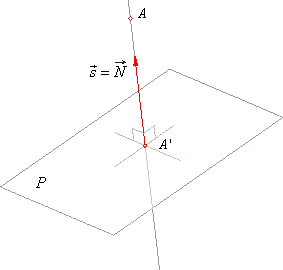
A given point A(x0, y0, z0) and its projection A′ determine a line of which the direction vector s coincides with the normal vector N of the projection plane P.
As the point A′ lies at the same time on the line AA′ and the plane P, the coordinates  of the radius (position) vector of a variable point of the line written in the parametric form 
x = x0 + a · t,  y = y0 + b · t and z = z0 + c · t,  
These variable coordinates of a point of the line plugged into the equation of the plane will determine the value of the parameter t  such that this point will be, at the same time, on the line and the plane.
 
Example:   Find the orthogonal projection of the point A(5, -6, 3) onto the plane 3x - 2y + z - 2 = 0.
Solution:  The direction vector of the line AA′ is s = N = 3i  - 2 j + k, so the parametric equation of the line which is perpendicular to the plane and passes through the given point A
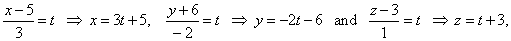
these coordinates of the radius vector of the point A′ must satisfy the equation of the given plane that is
3 · (3t + 5) - 2 ·  (-2t - 6) + 1 · (t + 3) - 2 = 0    =>     t = -2
therefore, the coordinates of the point A′ are,
x = 3t + 5 = 3 · (-2) + 5 = -1,    y = -2t - 6 = -2 · (-2)  - 6 = -2 and  z = t + 3 = -2 + 3 = 1,
thus the orthogonal projection of the point A onto the given plane is  A′(-1, -2, 1).
Projection of a point onto a line
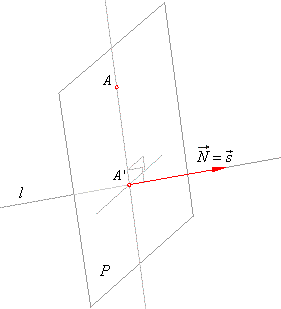
If we lay through a given point A a plane P perpendicular to a given line, then will the intersection of the line and the plane, at the same time be the projection A′ of the point onto the line. Then, the normal vector of the plane and the direction vector of the given line coincide, i.e.,
N = s
and since the coordinates of the given point must satisfy the equation of the plane, that way the plane is determined.
As the intersection A′ is the common point of the line and the plane then the parametric coordinates of a radius vector of the line plugged into the equation of the plane will determine the value of a parameter t such that this condition to be satisfied.
 
Example:   Find the projection of the point A(4, -2, 1) onto the line    
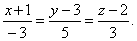Solution:  The normal vector of a plane, perpendicular to the given line, coincides to the direction vector of the line, that is N = s = -3i  + 5 j + 3k. 
As the plane must pass through the point A, then
A(4, -2, 1)   =>    -3x + 5y  + 3z  + D = 0   =>    -3 · 4 + 5 · (-2) + 3 · 1  + D = 0,    D = 19
Since the intersection is the common point of the given line and the plane then the coordinates of the radius vector of the intersection must satisfy the equation of the plane that is,
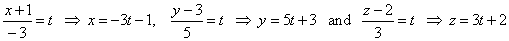
and plugged into the plane
-3 · (-3t - 1) + 5 · (5t + 3) + 3 · (3t + 2)  + 19 = 0,    t = -1
Thus, the coordinates of the intersection or the projection A′ are,
x = -3 ·  (-1) - 1 = 2,    y = 5 · (-1) + 3 = -2  and  z = 3 ·  (-1) + 2 = -1,    A′(2, -2, -1).
Coordinate geometry contents
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.